Underfitting e overfitting
Quando tentamos prever um valor \( y \) a partir de um conjunto de treino, podem-se ocorrer alguns problemas relacionados a função de hipótese. Esses problemas são chamados de underfitting e overfitting. Para explicá-los, podemos nos basear na Figura 13
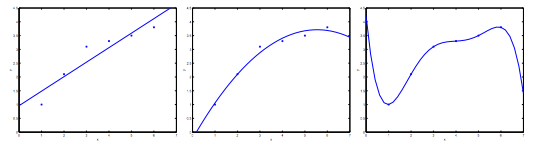
Figura 13: Representação dos problemas de underfitting e overfitting
Como podemos perceber, na figura mais à esquerda, temos uma função linear do tipo \( y= \theta _0 + \theta _1x \) que não seja ajusta adequadamente com a nossa base de treino. Na figura do centro temos uma função quadrática do tipo \( y= \theta _0 + \theta _1x + \theta _2x ^2 \), que aparentemente se adapta muito bem a nossa base de dados. E na figura mais à direita, temos um polinômio de grau cinco que atinge todos os pontos da nossa base de dados.
Com isso, podemos dizer que a figura mais à esquerda apresenta o problema de subajuste (underfitting ou high bias) e a figura mais à direita apresenta o problema de sobreajuste (overfitting ou high variance).
O problema de underfitting ocorre quando a função hipótese \( h \) não consegue mapear com consistência os valores da saída pois uma função muito simples é utilizada ou foram utilizados poucos parâmetros de entrada.
De outra forma, o problema de overfitting ocorre quando a função hipótese se adapta perfeitamente a nossa base de treino, mas não consegue generalizar os resultados das entradas. Isso ocorre, pois uma função muito complexa foi utilizada ou o número de parâmetros utilizados como entrada da função é muito alto.
Assim, temos alguns métodos que podemos utilizar para evitar esse tipo de problema. Dois são principais e estão listados abaixo:
-
Reduzir o número de parâmetros:
-
Manualmente selecionar os parâmetros a serem removidos;
-
Usar algoritmo de modelo de seleção [16].
-
-
Regularização (Regularization):
- Manter todos os parâmetros, mas reduzir a magnitude dos parâmetros de \( \theta _j \);