Stochastic Gradient Descent (SGD)

SGD é uma alternativa mais eficiente e escalável ao método clássico de otimização gradiente des- cendente.

SGD pode ser escrito de maneira muito similar ao método de gradiente descendente clássico, visto.

\[ \large{} cost(\theta , (x ^{(i)}, y ^{(i)})) = \frac{1}{2}(h _{\theta}(x ^{(i)}) - y ^{(i)}) ^2 \]

A principal diferença entre o método clássico e o SGD é que o SGD considera cada exemplo de treino individualmente para calcular o custo antes de realizar a média dos custos, enquanto o método clássico calcula o custo de acordo com a média dos valores.

Com isso, podemos definir a função custo da seguinte forma:

\[ \large{} J _{train}(\theta) = \frac{1}{m} \sum _{i=1} ^m cost(\theta , (x ^{(i)}, y ^{(i)})) \]

\( J _{train} \), agora, é apenas a média dos custos aplicado a todos os exemplos de treino.

Com esse tipo de metodologia, podemos otimizar o cálculo das derivadas parciais a fim de reduzir a função custo. Devido ao fato desse método ser estocástico, adicionamos aleatoriedade nas escolhas dos custos dos exemplos de treino. Para cada uma dessas escolhas, otimizamos os valores dos custos o que reduz de forma muito mais eficiente a complexidade da computação. Portanto, com o SGD, computamos a atualização do parâmetro \( \theta \) para cada um dos exemplos de treino \( x _i \) em relação ao seu rótulo \( y _i \), como podemos verificar abaixo:

\[ \large{} \theta = \theta - \alpha \cdot \nabla _{\theta} J(\theta ; x ^{(i)}; y ^{(i)}) \]

onde \( \alpha \) é a taxa de aprendizado e \( \nabla \) é o gradiente do custo \( J \).

Podemos visualizar na Figura 37 as diferenças entre as etapas de aprendizado entre o método clássico do gradiente descendente e o método estocástico. Percebemos, que SGD é mais "barulhento" em relação ao método clássico, porém, como não precisamos calcular as derivadas para cada um dos \( m \) m exemplos de treino por iteração, o SGD acaba sendo mais eficiente.

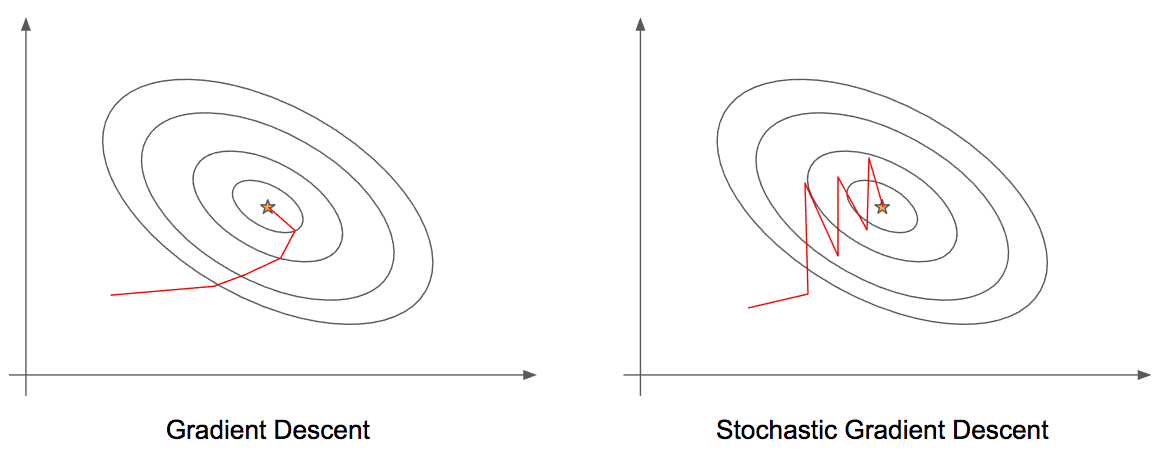
Figura 37

O algoritmo de SGD é muito similar ao algoritmo clássico, iremos atualizar os parâmetros \( \Theta _j \) ao longo do aprendizado de acordo com a função custo, como segue:

Algorithm 10 Algoritmo Stochastic Gradient Descent (SGD)

1: procedure

2:   Aleatoriamente,"misturar" o conjunto de dados

3:   for \( i = 1 \) to \( m \) do

4:    \( \theta _j := \theta _j - \alpha (h _{\theta}(x ^{(i)}) - y ^{(i)}) \cdot x _j ^{(i)} \)

5:   end for

6: end procedure

Esse algoritmo, diferentemente do método clássico, ajustará um exemplo de treino por vez. Com isso, podemos prosseguir com o algoritmo de gradiente descendente, sem, necessariamente examinar todos os \( m \) exemplos de treino antes.

Um dos problemas desse algoritmo é que, muitas vezes, ele não convergirá para o mínimo global do problema e, ao invés disso, irá vagar aleatoriamente ao redor desse mínimo, porém, na maioria das vezes, produz um retorno muito próximo ao esperado. Normalmente, o SGD varre o conjunto de dados entre uma ou dez vezes antes de chegar próximo ao mínimo global. Como podemos perceber na Figura 38, o SGD pode acabar travado em um mínimo local e isso resulta em dificuldade em otimizar ao máximo a função custo, pois o algoritmo não irá convergir para o mínimo global.

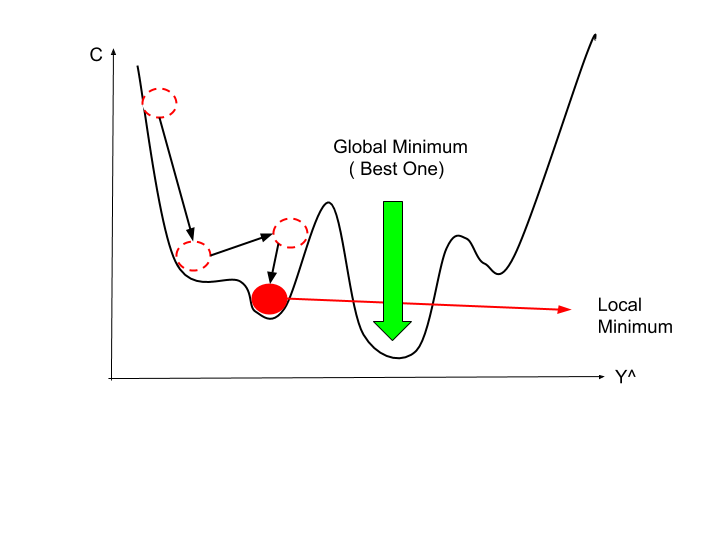
Figura 38: Representação da dificuldade de convergência do algoritmo SGD. Percebe-se que a minimização da função custo atinge um mínimo local devido às "voltas" que o algoritmo dá ao redor do mínimo global.

Podemos evitar esse tipo de problema incentivando a convergência do algoritmo. Para isso, podemos escolher valores de α diferentes a cada iteração, diminuindo o seu valor.

Com uma taxa de aprendizado menor, o algoritmo irá oscilar de maneira mais suave, sem grandes pulos em torno do mínimo global. Dessa forma, uma estratégia seria diminuir o valor de \( \alpha \) a cada iteração, como segue:

\[ \large{} \alpha = \frac{const1}{iterationNumber+const2} \]

Todavia, esse método não é muito utilizado devido a quantidade extra de parâmetros que devem ser ajustados.