Aplicações
Mas afinal, para que uma rede neural pode ser útil? Ao longo das últimas décadas, a área de pesquisa que envolve redes neurais está se desenvolvendo de maneira significativa. Apesar desse desenvolvimento ainda estar no começo, já foram descobertas diversas aplicações de redes neurais, como podem ser vistas a seguir:
-
Computer Vision: reconhecimento de objetos, emoções, etc;
-
Natural Language Processing (NLP): reconhecimento de discursos e tradução de idiomas;
-
Deep Q-Network (DQN) e Asynchronous Actor-Critic Agents (A3C) para reinforcement learning, como por exemplo Atari;
-
AlphaGo [19];
-
Aesthetic quality assessment
Para o melhor entendimento do tipo de implementação que uma rede neural linear com apenas duas camadas - input e output - podemos criar um vetor para \( \Theta ^{(1)} \) para computar a função \( x _1 AND x _2 \) da seguinte forma:
\[ \large{} \Theta ^{(1)} = \begin{bmatrix} -30 && 20 && 20 \end{bmatrix} \]
Percebemos que no exemplo não temos hidden layers. Temos a input layer seguida pelo processamento da função hipótese.
Como sabemos que, pela função sigmoide, com uma entrada de duas variáveis \( x _1 \) e \( x _2 \) teremos valores binários (0 ou 1) na saída da função hipótese \( h _{\Theta}(x)=g(-30+20x _1 + 20x _2) \). Essa ideia pode ser representada na tabela a seguir:
Tabela 2: Implementação da rede neural usando portas 'and' \( x _1 AND x _2 \)
| \( x _1 \) | \( x _2 \) | \( h _{\Theta}(x) \) |
|---|---|---|
| 0 | 0 | \( g(-30) \approx 0 \) |
| 0 | 1 | \( g(-10) \approx 0 \) |
| 1 | 0 | \( g(-10) \approx 0 \) |
| 1 | 1 | \( g(10) \approx 1 \) |
Como vimos até agora, representamos redes neurais simples com duas camadas - input e output - chamadas de Perceptrons. Contudo, esse tipo de implementação possui diversas limitações. A primeira delas foi observada ao tentar implementar a função \( XOR \). Essa limitação potencializou a criação de novas arquiteturas de redes neurais, pois a função \( XOR \) não é linearmente separável, ou seja, não se pode, de maneira linear - com apenas duas camadas - representá-la em uma rede neural. A Figura 16, abaixo, representa o surgimento desse problema.
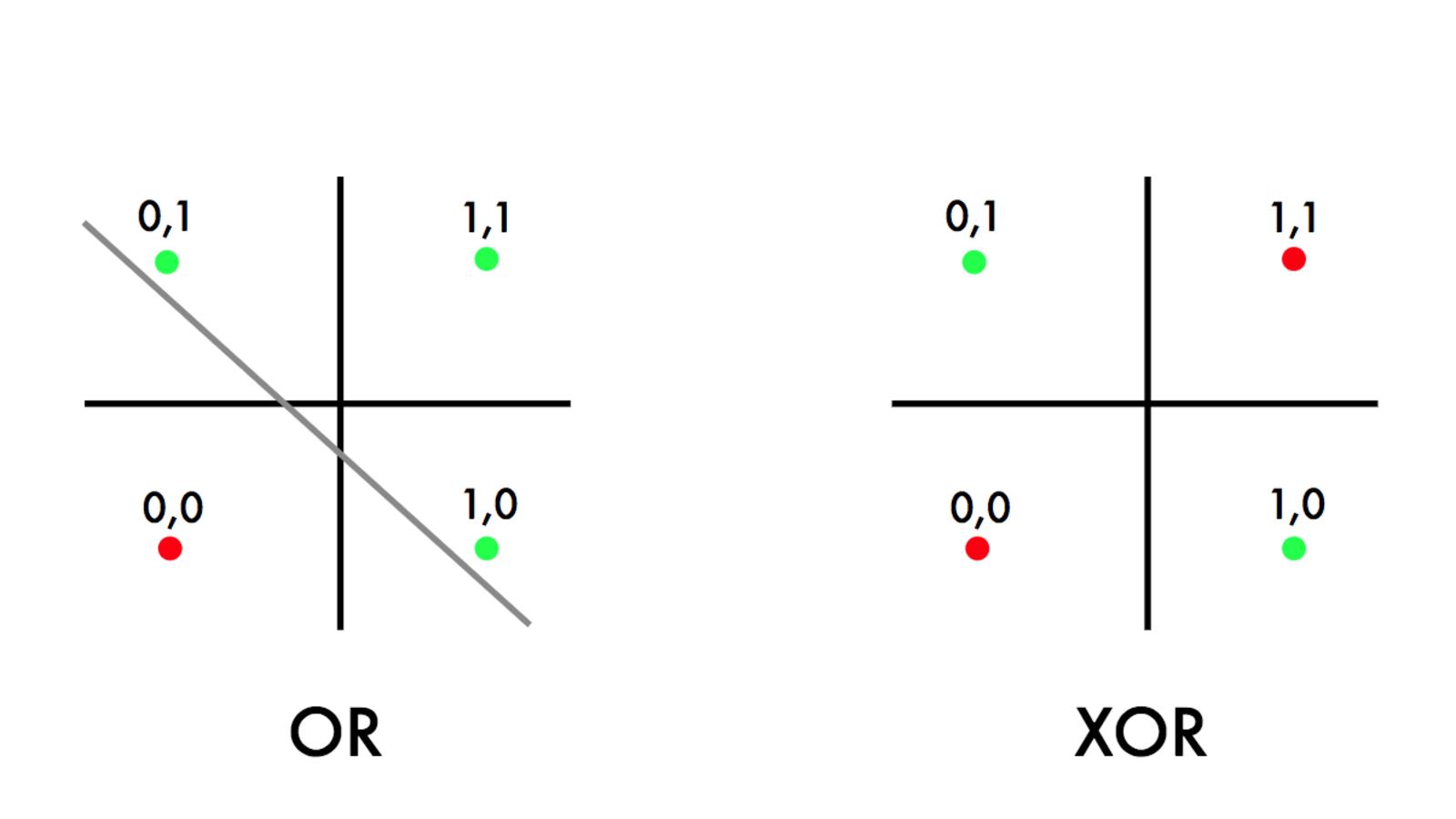
Figura 16: No gráfico da esquerda, percebemos a aplicação da função \( OR \), cujos pontos verdes representam a saída 1 e os vermelhos a saída zero. No gráfico da esquerda, percebemos a aplicação da função \( XOR \), cujos pontos possuem a mesma representatividade. Na função \( OR \), podemos traçar uma reta que divida as classes 0 e 1 do problema, enquanto na função \( XOR \) isso não é possível devido ao fato das classes não sejam linearmente separáveis.
Uma solução para este problema foi a criação de novas camadas internas, chamadas de hidden layers, que foram discutidas na Seção Representação do modelo, dando origem a uma nova arquitetura de rede neural chamada Multilayer perceptron (MLP). Na Figura 17 abaixo, está representada a arquitetura de rede neural para a resolução do problema \( XOR\).
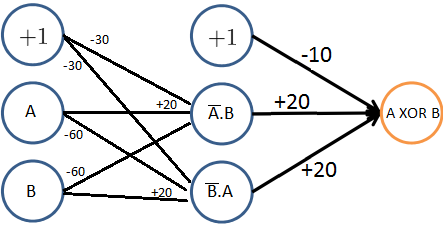
Figura 17: Representação da arquitetura que soluciona o problema \( XOR \). Neste caso, temos três camadas: input layer, hidden layer e output layer
A seguir, iremos discutir as diferentes arquiteturas de redes neurais para diferentes tipos de classifi- cação.