SGD + Momentum
Como foi explicado, um dos problemas do SGD é que muitas vezes, o algoritmo pode ficar "preso" em um mínimo local próximo do global e não convergir de forma adequada para o nosso problema. Para isso, uma forma de otimização foi utilizar momentum a fim de incentivar a convergência.
Antes de definir esse método de otimização, podemos intuitivamente compreender como funciona o momentum. Para isso, podemos pensar em uma bola que rola em uma colina do ponto mais alto ao mais baixo, seguindo a inclinação. Desejamos que essa bola tenha a noção de onde ela está indo. Essa intuição pode ser relacionada aos valores dos parâmetros que desejamos atualizar, ou seja, esses parâmetros se comportariam como se fossem a tal bola.
Uma boa definição para o momentum é que é uma média móvel dos nossos movimentos, ou seja, como determinado corpo se comporta em determinado terreno de acordo com a velocidade e a aceleração proporcionada pelo mesmo. Dessa forma, a cada etapa do processo de otimização da função custo, teremos vetores que representam o momentum do ponto em determinada parte do "terreno" da função custo, e esses vetores proporcionarão uma velocidade maior de convergência na direção a qual ele está apontando.
Na Figura 40 está representada a diferenciação no comportamento do SGD sem e com a utilização de momentum.
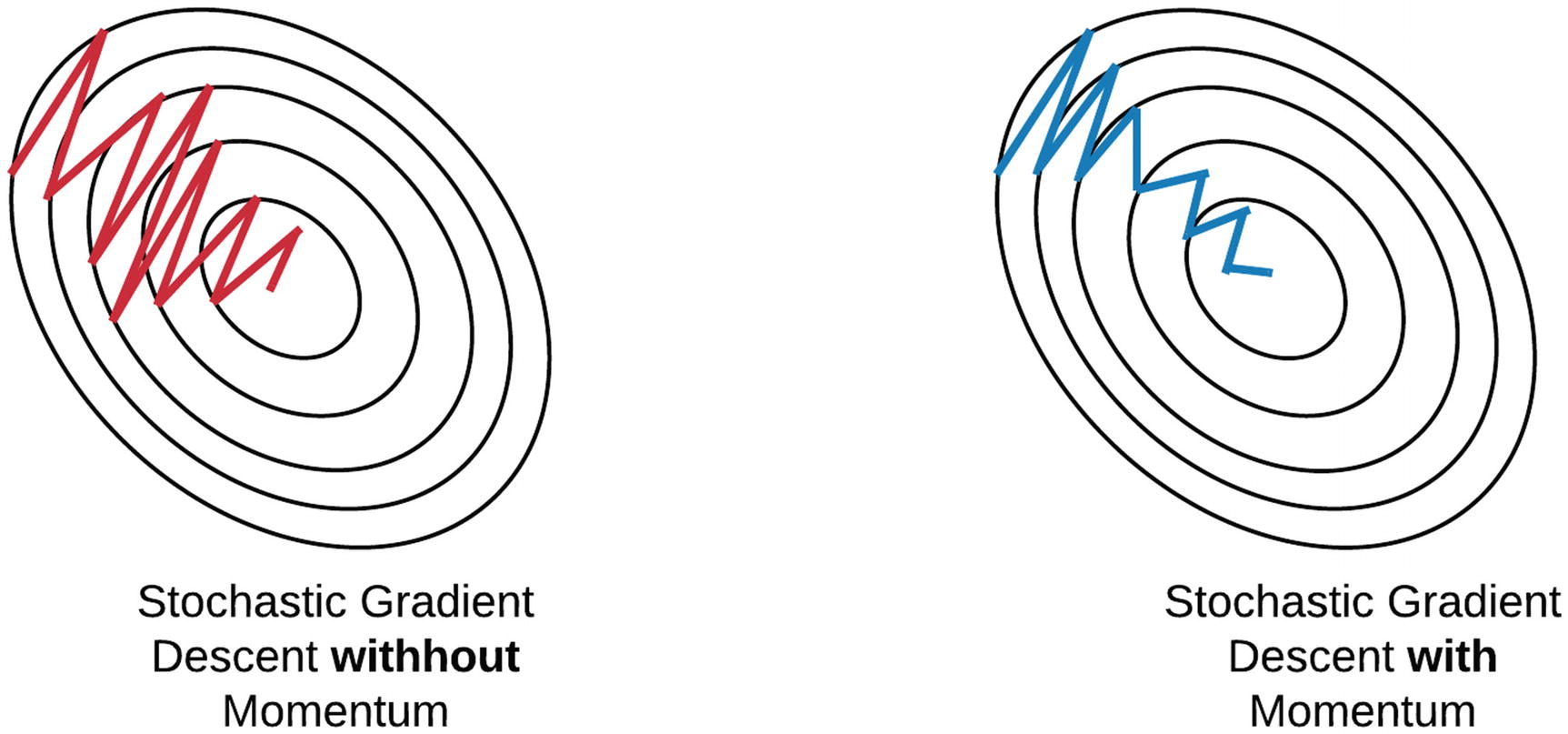
Figura 40: À esquerda representação no comportamento dos parâmetros sendo minimizados através do método SGD e à direita o mesmo método com a aplicação de momentum.
Podemos diferenciar os dois modelos de otimização da forma que segue:
| SGD | SGD + Momentum |
|---|---|
| \( x _{t+1} = x _t - \alpha \nabla f(x _t) \) | \( v _{t+1} = \rho v _t + \nabla f(x _t) \) |
| \( x _{t+1} = x _t - \alpha v _{t+1} \) |
Onde \( x _i \) representa os parâmetros a serem atualizados, \( v _i \) representa o momentum do ponto em determinada parte, \( \nabla f(x _i) \) representa o gradiente da função custo e \( \rho \) representa o atrito do ponto em determinada parte (geralmente esse parâmetro é definido como 0.9 ou 0.99).
Contudo, um dos problemas que esse método de otimização proporciona é que, muitas vezes, quando os parâmetros se aproximam do mínimo, devido ao momentum, demoram para convergir pois ultrapassam esse mínimo. Para resolver esse problema, devemos desacelerar a atualização desses parâmetros de acordo que eles se aproximam do mínimo, o que será visto na seção seguinte.