Deep Q-Learning
Como foi visto na Seção Aprendizado por reforço (Reinforcement learning), através do método de Q-learning, atualizamos os valores das políticas do agente maximizando os valores de Q de acordo com o estado futuro do ambiente e da ação tomada, de maneira recursiva, usando a equação de Bellman.
Contudo, apesar do grande poder desse método, de acordo com a complexidade do ambiente, ele pode ser tornar extremamente ineficiente. Para resolver esse problema, usamos um método que engloba Q-learning e redes neurais profundas, chamado Deep Q-learning (DQN).
De maneira geral, ao invés de trabalharmos com uma tabela para atualizar os valores de Q de decisão de ação do agente, utilizamos uma rede neural. Essa rede neural funciona através de uma função de aproximação, chamada de aproximador, denotado por \( Q(s, a; \theta) \), em que \( \theta \) representa os pesos treináveis da rede, para aproximar os valores de Q de forma ótima.
Assim, a equação de Bellman, vista na Seção Q-Learning é utilizada como a função custo, que deve ser minimizada. Em outras palavras, minimizamos a diferença entre a igualdade do valor Q que deve ser atualizado em relação a soma da recompensa com o desconto do máximo valor de Q dos estados futuros. Ou seja,
\[ \large{} Cost = \Big[ Q(s,;\theta) - \Big( r(s,a) + \gamma \ \underset{a}{max} \ Q(s',a;\theta) \Big) \Big] ^2 \]
onde \( Q(s,;\theta) \) é chamado de Q-target, os parâmetros da rede neural.
O treinamento desse tipo de rede neural acontece durante o momento de exploration e exploitation, atualizando os valores de Q já vistos e que serão descobertos futuramente. Para o treino, portanto, selecionamos \( b \) estados já visitados, juntamente com os seus respectivos valores, de maneira aleatória, e usamos esses valores como input e target, respectivamente.
Diferentemente do método de Q-learning tradicional, DQN prevê os \( N \) possíveis valores de Q para um determinado estado. Na Figura 98 abaixo, está representada essa diferença entre os dois métodos.
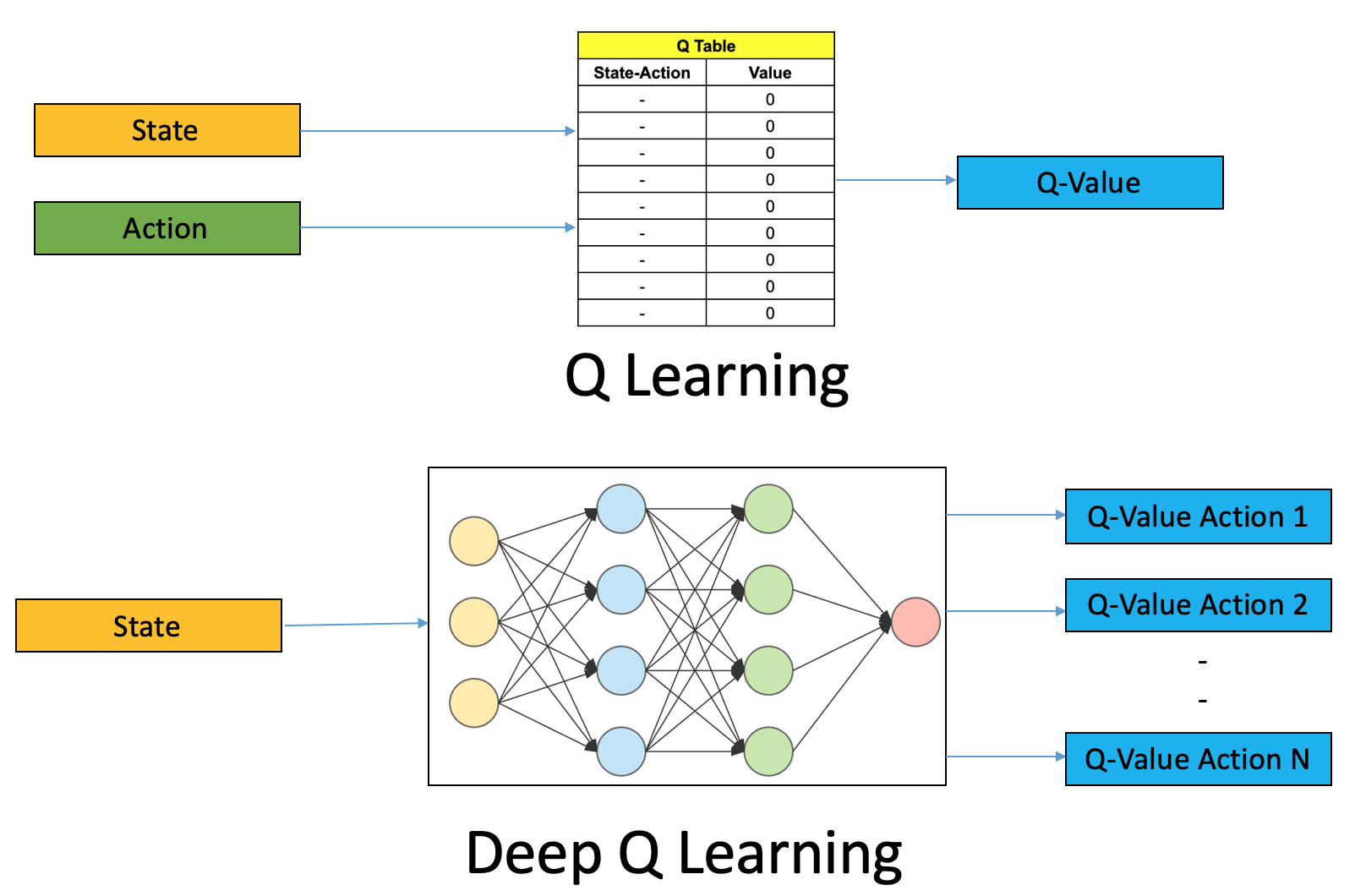
Figura 98: Representação dos dois métodos de Q-learning. Na figura do topo, a partir de uma determinada ação tomada em um estado de ambiente, gera-se um valor de Q referente a este par estado-ação. Na figura de baixo, dado um estado, a rede neural calcula todos os valores de Q referentes a todas as ações possíveis a serem tomadas, selecionando o melhor valor para aquele estado.
Com isso, podemos listar as etapas que envolvem o aprendizado de uma rede neural.
-
Passar como entrada estado atual \( s \) do ambiente para a rede neural. Essa rede neural irá retornar os valores Q de todas as possíveis ações a serem tomadas pelo agente no estado \( s \).
-
Selecionar uma ação usando a política \( \epsilon \)-greedy. Com a probabilidade \( \epsilon \), selecionar uma ação aleatória \( a \) (exploration) e com a probabilidade \( 1 - \epsilon \) escolher a ação que corresponde o valor máximo de Q, tal que \( a = argmax(Q(s,a;\theta)) \)
-
Realizar a ação tomada \( a \) no estado \( s \) e mover para o próximo estado \( s' \) para receber a recompensa.
-
Após, tomamos uma decisão aleatória de transição de estado e calculamos o custo
-
Minimizar o erro da função custo utilizando algum método de otimização, como por exemplo, gradiente descendente
-
A cada \( C \) iterações, copiar os pesos da rede neural atual para uma rede neural target a fim de salvar os pesos
-
Repetir esses passos \( M \) episódios
Com DQN, temos uma ferramenta extremamente forte para resolução de problemas de aprendizado de RL. Agora, com ambientes mais complexos e com mais interações, o agente consegue realizar uma melhor valoração das possibilidades de ações que podem ser tomadas baseadas no retorno da rede neural. Atualmente, jogos de Atari, Go e StarCraft já atingiram níveis humanos de comportamento utilizando DQN e outros métodos de IA.