Self-Attention

Segundo a definição de Ashish Vaswani et al. [21] do Google Brain, "Self-attention, às vezes chamado de intra-attention, é um mecanismo de atenção relacionado a diferentes posições de uma única sequência que tem como objetivo computar uma representação para a sequência".

Self-attention nos possibilita encontra correlações entre diferentes palavras de entrada indicando a estrutura contextual e sintática da sentença.

Na prática, o transformer possui três representações de attention formadas por matrizes denominadas Queries, Keys e Values resultantes da camada de embedding. Essa representação é chamada de Multi-head attention (Figura 83).

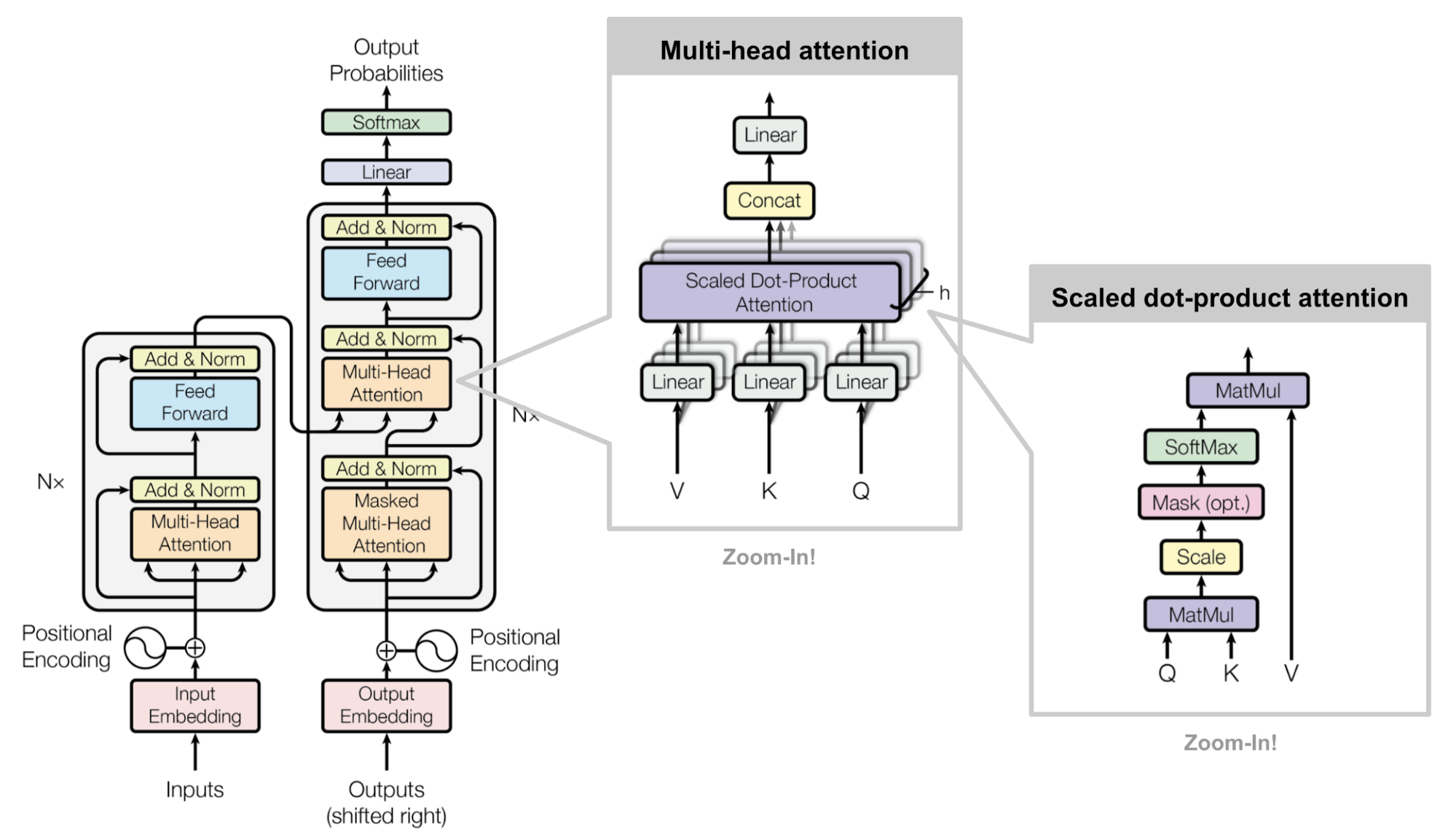
Figura 83: Representação de multi-head attention em um transformer. Os símbolos Q, K e V representam, respectivamente as matrizes Queries, Keys e Values.

O princípio básico da criação dessa camada é o descobrimento de relações semânticas nas sentenças. Após a camada de embedding, os vetores expressam a relação entre cada uma das palavras e, a partir desse contexto, a camada de multi-head attention tem como objetivo relacionar a palavra que estamos buscando (Q) com as palavras que possam estar relacionadas com ela (K) e, por fim, influenciar a decisão de acordo com a palavra que gostaríamos que fosse retornada (V).

Essas matrizes, inicialmente, são todas iguais quando passadas como entrada para a linear layer (por isso o nome self-attention). Essa linear layer, tem como objetivo diferenciar cada uma dessas três matrizes Q, K e V multiplicando cada uma delas por três matrizes de pesos da distintos \( W _Q , W _K , W _V \), um para cada uma das linear layers.

Para comparar a palavra que estamos buscando Q com os seus possíveis relacionamentos K, reali- zamos uma operação vetorial que calcula o cosseno do ângulo entre essas palavras. Esse ângulo, como vimos na Vetores de palavras (word embeddings) representa o quão relacionadas semanticamente essas palavras estão. Genericamente, o cálculo do cosseno entre dois vetores se dá por

\[ \large{} \cos (A,B) = \frac{A \cdot B}{|A| |B|} \]

Com isso em mente, a primeira tarefa que devemos realizar é encontrar os relacionamentos entre as matrizes Q e K. Para isso realizamos o produto entre essas matrizes (numerador da equação acima) a fim de gerar um filtro de atenção e dividimos pela raiz quadrada tamanho da sentença \( \sqrt{d _k} \) (denominador da equação acima). Por fim, os resultados dessa matriz é passado para uma camada de ativação softmax (Seção Camada de ativação: Hyperbolic tangent) a fim de gerar valores de probabilidade dos relacionamentos entre as palavras. Essas operações irão gerar um filtro de atenção que irá prestar atenção em uma parte específica da sentença baseando-se no relacionamento entre cada uma das palavras.

Para facilitar a compreensão, podemos fazer um paralelo com a atuação de um filtro de atenção sobre uma imagem. O que acontece, neste caso é que ignoramos todos os pixels da imagem original que não interferem no resultado que desejamos alcançar. A Figura 84 abaixo, representa a aplicação do filtro de atenção gerado sobre uma imagem original. O resultado dessa aplicação é uma imagem em que somente o que realmente interessa está aparecendo.

Figura 84: Exemplificação da aplicação de um filtro de atenção sobre os valores dos pixels de uma imagem.

Nesse sentido, de acordo com a imagem acima, attention filter é o filtro gerado através das multi- plicações de matrizes, escalonamento e softmax realizadas com as matrizes Q e V e original image é a entrada do mecanismo de self-attention, ou seja, a matriz V. Portanto, para a gerar a imagem filtrada, realizamos, basicamente, uma multiplicação entre o filtro de atenção gerado pelas matrizes Q e K e o conteúdo de entrada V.

Com isso, temos, finalmente, a equação desse mecanismo de self-attention, descrita abaixo.

\[ \large{} Attention (Q,K,V) = softmax \Big( \frac{QK ^T}{\sqrt{d _k}} \Big) V \]