Variational Autoencoders (VAE)
Como vimos até agora, PixelCNNs definem a função de densidade travável e otimiza a probabilidade de dados de treinamento. De outra forma, VAEs definem funções de probabilidade intratáveis de acordo com um valor \( z \) que é chamado de espaço latente e será definido posteriormente.
Dessa forma, um VAE é um Autoencoder cuja distribuição de codificações é regularizada durante o treinamento, a fim de garantir que seu espaço latente tenha boas propriedade, o que nos permite gerar novos dados
Em geral, Autoencoders são redes neurais para redução de dimensionalidade. A estrutura básica de um Autoencoder está representada na Figura 91 Essas redes neurais tem como objetivo aprender o melhor esquema de codificação-decodificação usando um processo de otimização iterativo.
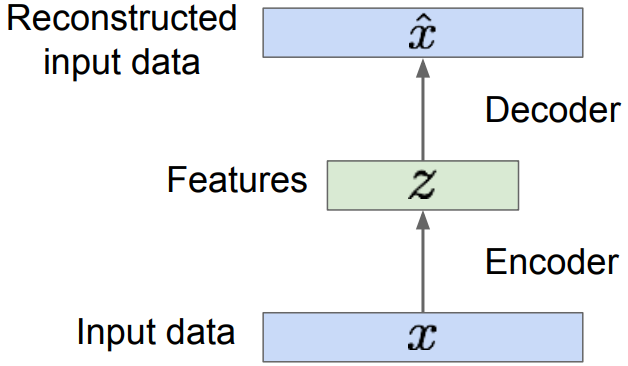
Figura 91: Através de dados de entrada x treinamos o nosso modelo de forma que possamos reconstruir os dados originais através do Autoencoder. Dessa forma, z são os dados de entrada codificados através de algoritmos de redução de dimensionalidade e x̂ é o conjunto de dados decodificado a partir de z.
Assim, a arquitetura geral de um Autoencoder cria um gargalo de dados que garante que apenas a parte estruturada principal da informação possa ser reconstruída. Os codificadores e decodificadores são transformações lineares simples que podem ser expressas como matrizes, da mesma forma que o algoritmo PCA funciona e no final, adicionamos não-linearidade.
Autoencoders são, portanto, arquiteturas de codificador-decodificador que podem ser treinadas uti- lizando um algoritmo de otimização como, por exemplo, gradiente descendente.
Finalmente, podemos definir um VAE. VAE é uma arquitetura composta por um codificador e um decodificador treinada para minimizar o erro de reconstrução entre os dados decodificados e os dados iniciais. Assim, podemos treinar o modelo da seguinte forma:
-
A entrada é codificada como distribuição do espaço latente \( z \)
-
Um ponto do espaço latente é amostrado a partir dessa distribuição
-
O ponto amostrado é decodificado e o erro de reconstrução pode ser calculado
-
Backpropagation utilizando o erro de reconstrução
Na Figura 92 a seguir, está esquematizado o processo de treino do modelo, sabendo que \( x \) representa os dados de entrada, \( z \) o espaço latente e \( d(z) \) a reconstrução da entrada.

Figura 92
Com isso, a função custo que é minimizada ao treinar um VAE é composta por um ”termo de reconstrução” que torna o esquema de codificação-decodificação mais eficiente e um ”termo de re- gularização” que regulariza a organização do espaço latente, tornando-a mais próxima da Distribuição Normal Padrão. Esse termo é expresso como a divergência de Kullback-Leibler, que sua definição não faz parte do escopo deste curso.
A seguir, na Figura 93 está esquematizada uma estrutura básica de um VAE com a definição da sua função custo, que são dependentes dos valores de entrada \( x \), da distribuição do espaço latente \( N(\mu _x , \sigma _x ^2) \) e da aproximação gerada a partir do espaço latente \( x̂ = d(z) \).
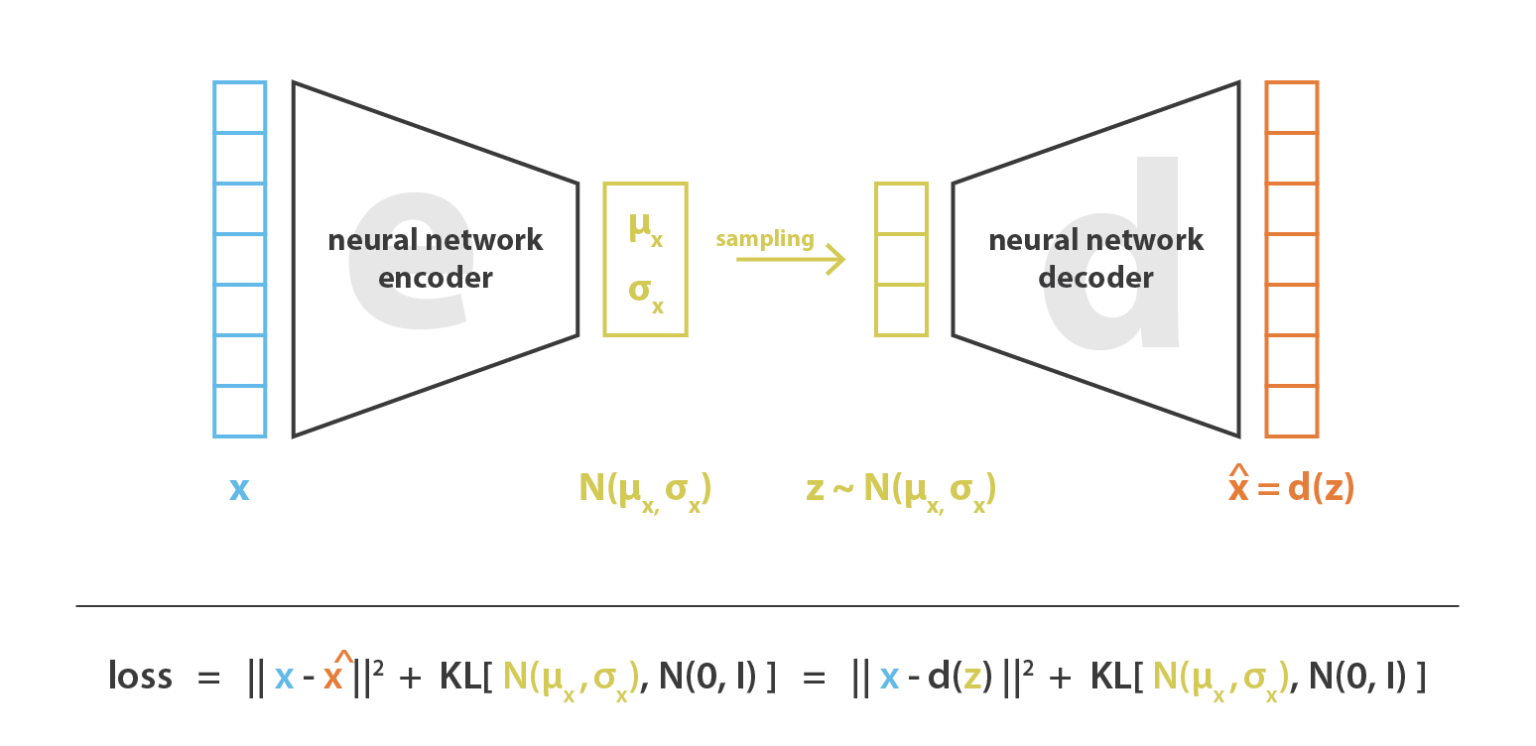
Figura 93
Portanto, através de VAEs podemos utilizar amostras usadas no espaço latente para gerar dados similares através do decodificador. A figura abaixo mostra os dados gerados a partir de uma rede decodificadora de um VAE treinada a partir da base de dados MNIST. Além disso, um dos pontos negativos da utilização de VAEs é que as amostras geradas são embaçadas e de baixa qualidade. Portanto para a melhoria da qualidade utilizamos GANs, que serão descritas a seguir.

Figura 94: Nesta imagem estão representados os dígitos gerados por uma rede VAE através do decodificador. A imagem tem esse padrão devido a forma bidimensional da Distribuição Normal. Como se pode perceber, os dígitos distintos estão em diferentes regiões da imagem devido ao espaço latente.