K-Means Algorithm
K-Means Algorithm é um dos algoritmos mais populares e são amplamente utilizados a fim de, automaticamente, agrupar dados em subgrupos denominados clusters.
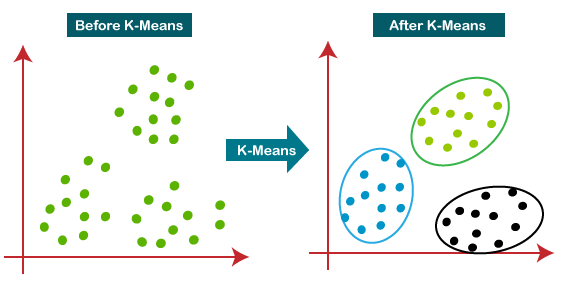
Figura 29: Representação de clustering através do algoritmo de K-Means. Percebe-se que, com a aplicação do algoritmos os dados passam a formar conjuntos diferentes, na figura, representados pelas cores azul, verde e preto.
Antes de discutir o algoritmo, podemos discutir o funcionamento desse método de machine learning para os três clusters da imagem acima.
-
Randomicamente inicializar três pontos no conjunto de dados. Esses pontos serão chamados de cluster centroids;
-
Atribuição do cluster: atribua todos os exemplos em um dos três grupos baseado em qual centroid os exemplos estão mais próximos;
-
Mover os centroids: computar as médias de todos os pontos dentro de cada um dos três centroids, e mover os centroids para os pontos que representam as médias;
-
Executar os passos (2) e (3) até convergir.
Para o algoritmo, teremos as seguintes variáveis principais:
-
\( K \): número de clusters;
-
\( x ^{(1)}, x ^{(2)}, \dots , x ^{(n)} \): conjunto de treino, onde \( x ^{(i)} \in \mathbb{R} ^n \)
Algorithm 8 Algoritmo K-Means
1: procedure
2: Randomicamente inicializar \( K \) cluster centroids \( \mu _1, \mu _2, \dots , \mu _K \in \mathbb{R} ^n \)
3: repeat
4: for \( i=1 \) to \( m \) do
5: \( c ^{(i)} := \) índice (de 1 até \( K \)) do cluster centroid mais perto de \( x ^{(i)} \)
6: end for
7: for \( k=1 \) to \( K \) do
8: \( \mu _k := \) média dos pontos atribuídos ao cluster \( k \)
9: end for
10: until \( convergir \)
11: end procedure
No algoritmo, percebemos que existem dois loops. O primeiro, realiza a etapa (2) descrita acima da seguinte forma:
\[ \large{} c ^{(i)} = argmin _k || x ^{(i)} - \mu _k || ^2 == || (x _1 ^i - \mu _{i(k)}) ^2 + (x _2 ^i - \mu _{2(k)}) ^2 + \dots || \]
No segundo loop realiza a etapa (3) e pode ser descrita da seguinte forma:
\[ \large{} \mu _k = \frac{1}{n} [x ^{(k _1)} + x ^{(k _2)} + \dots + x ^{(k _n)}] \]
Onde cada valor de \( x ^{(k _1)},x ^{(k _2)}, \dots ,x ^{(k _n)} \) são os exemplos de treino atribuidos por \( \mu _k \)
Depois de um número de iterações, o algoritmo irá convergir e as posições dos centroids não serão mais alteradas.