Distribuição Gaussiana

A Distribuição Gaussiana, ou Distribuição Normal, é uma forma de distribuição uniforme em formato de sino que pode ser descrita através de uma função \( N(\mu , \sigma ^2) \). Onde, dado um valor \( x, x \sim N(\mu , \sigma ^2) \), representa a probabilidade na distribuição de \( x \), com média \( \mu \) e variância \( \sigma ^2 \).

A Distribuição Gaussiana, então, é parametrizada pela média e pela variância do conjunto de dados (Figura 36).

Além disso, \( \mu \) representa o centro da curva (média) e a largura da distribuição é descrita por \( \sigma \) (desvio padrão).

A função da Distribuição Gaussiana é definida da seguinte forma:

\[ \Large{} p(x; \mu , \sigma ^2) = \frac{1}{\sigma \sqrt{(2 \pi)}} e ^{- \frac{1}{2} (\frac{x - \mu}{\sigma}) ^2} \]

Podemos estimar o parâmetro \( \mu \) de um dado conjunto de dados apenas calculando a média do todos os exemplos:

\[ \large{} \mu = \frac{1}{m} \sum _{i=1} ^m x ^i \]

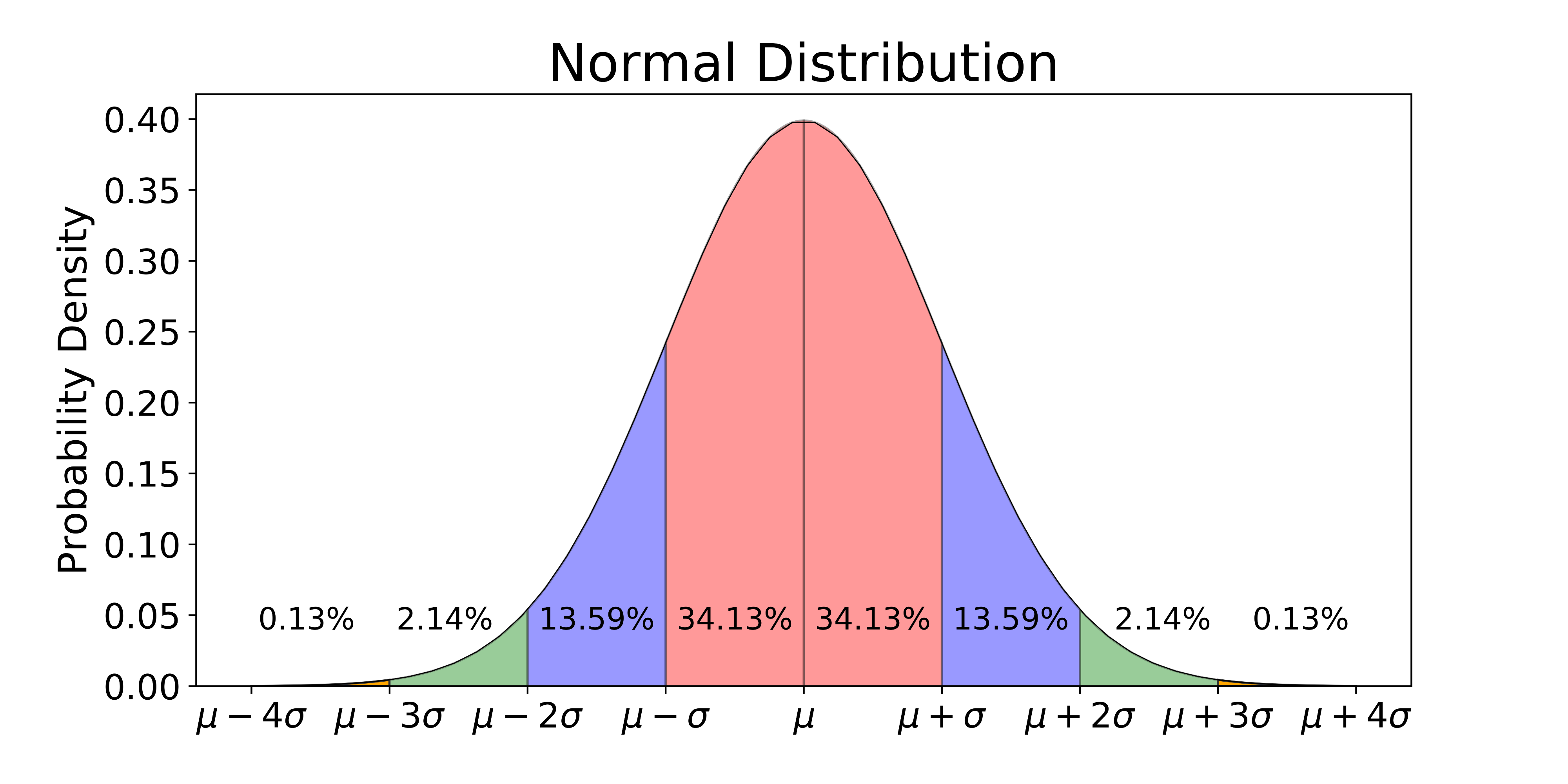
(a) Representação da Distribuição Gaussiana. O eixo \( x \) representa os valores dos exemplos de acordo com a média e com a variância e o eixo \( y \) representa a densidade de probabilidade o exemplo.

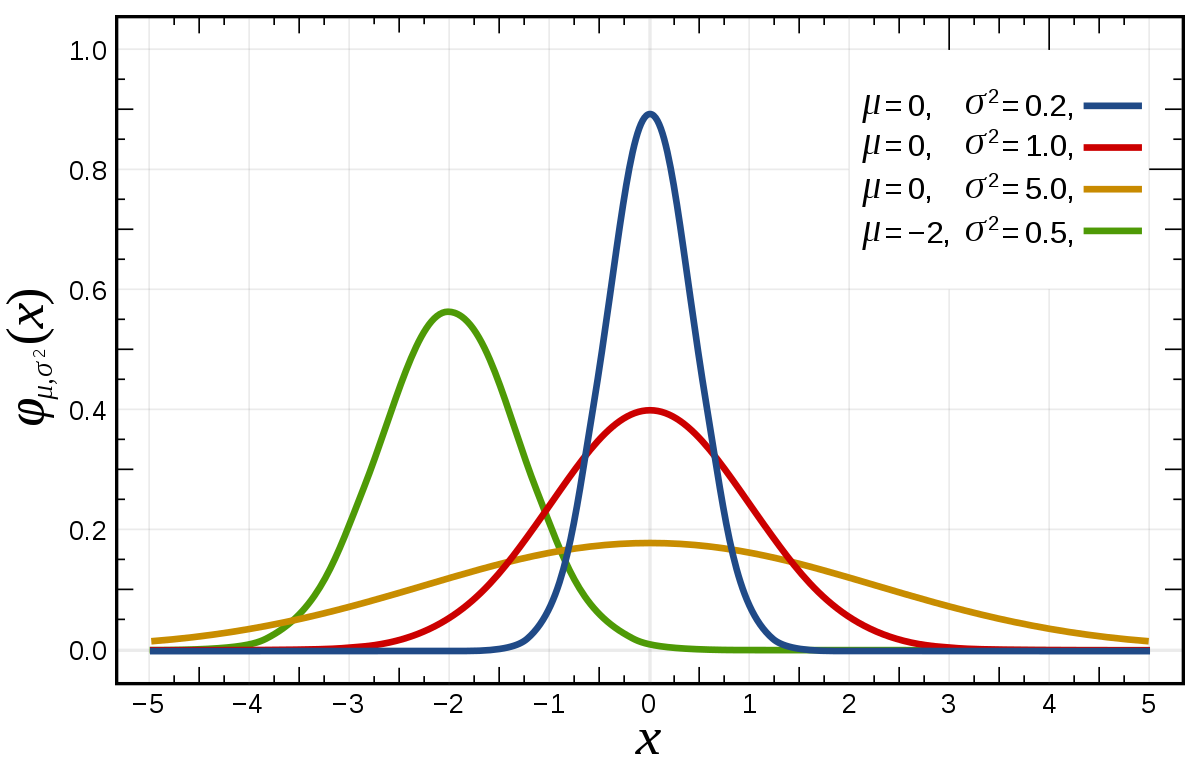
(b) Representação de diferentes estruturas distribuições gaussianas de acordoc om os valores dos parâmetros \( µ \) e \( \sigma ^2 \) . Podemos perceber o efeito da alteração desses parâmetros nas estruturas das curvas.

Figura 36

Da mesma forma, podemos estimar o parâmetro \( \sigma ^2 \) através da fórmula de erro quadrático a qual já estamos familiarizados.

\[ \large{} \sigma ^2 = \frac{1}{m} \sum _{i=1} ^m (x ^i - \mu) ^2 \]