Representação da hipótese

Podemos utilizar o nosso antigo algoritmo de regressão linear para prever um valor de \( y \) discreto dado um valor de \( x \). Mas como foi mencionado anteriormente, essa não é uma boa solução para problemas de classificação e para isso, devemos modificar a função hipótese a fim de satisfazer a saída discreta dos problemas de classificação, ou seja, \( 0 \geq h _{\theta}(x) \geq 1 \).

Uma boa modificação seria basear a nossa função hipótese na função logística (Logistic Function) de forma que possamos nos basear na função sigmoide conforme representada na Figura 10. Em outras palavras, teremos:

\[ \large{} h _{\theta}(x) = g(\theta ^T x), \ z = \theta ^T x, \ g(z) = \frac{1}{1 + e ^{-z}} \]

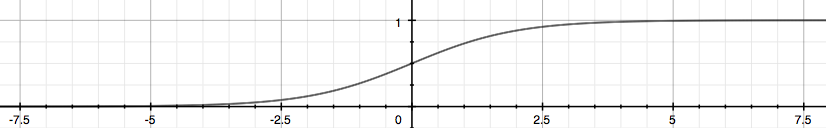
Figura 10: Representação da função sigmoide

A função sigmoide mapeia um valor real em um valor no intervalo \( (0,1) \) fazendo com que seja a melhor forma de implementação de problemas de classificação.

Dessa forma, podemos chegar a algumas conclusões e interpretações dessa nova forma de implementação da função hipótese:

• \( h _{\theta}(x) \) nos dá a probabilidade da nossa saída ser 1.

• \( h _{\theta}(x)=P(y=1|x; \theta )=1-P(y=0|x; \theta )P(y=0|x; \theta )+P(y=1|x; \theta )=1 \)