Representação do modelo
A partir de uma análise biológica do cérebro humano, sabemos que dois neurônios se comunicam através de impulsos nervosos chamados de sinapses. A informação recebida por um neurônio passa, primeiramente, pelos dendritos e vai em direção ao axônio. Podemos modelar essas informações a fim de gerar um modelo matemático que represente um neurônio da seguinte forma:
-
Dendrito: entrada da função \( (x _1, \dots , x _n) \);
-
Axônio: função hipótese \( (h _{\theta}(x)) \);
Nas redes neurais, utilizamos a mesma função utilizada na regressão logística \( \large{} \frac{1}{1+e ^{-z}} \), a qual chamamos de "ativação" da função e os parâmetros \( \Theta \) são chamados de "pesos". Podemos perceber na Figura 15 que o neurônio possui três camadas, as quais chamamos de camada de entrada (input layer), camada escondida (hidden layer) e camada de saída (output layer). A camada de saída também pode ser chamada de função hipótese \( h _{\Theta} \).
Com isso, devemos adicionar algumas notações relacionadas às redes neurais.
-
Chamamos de \( x _0, x _1, \dots , x _n \) os valores da input layer, onde \( x _0 = 1 \) (bias unit);
-
\( a _i ^{(j)} \) é unidade de "ativação" \( i \) na camada \( j \);
-
\( \Theta ^{(j)} \) é a matriz de pesos que controla o mapeamento da função da camada \( j \) para a camada \( j+1 \).
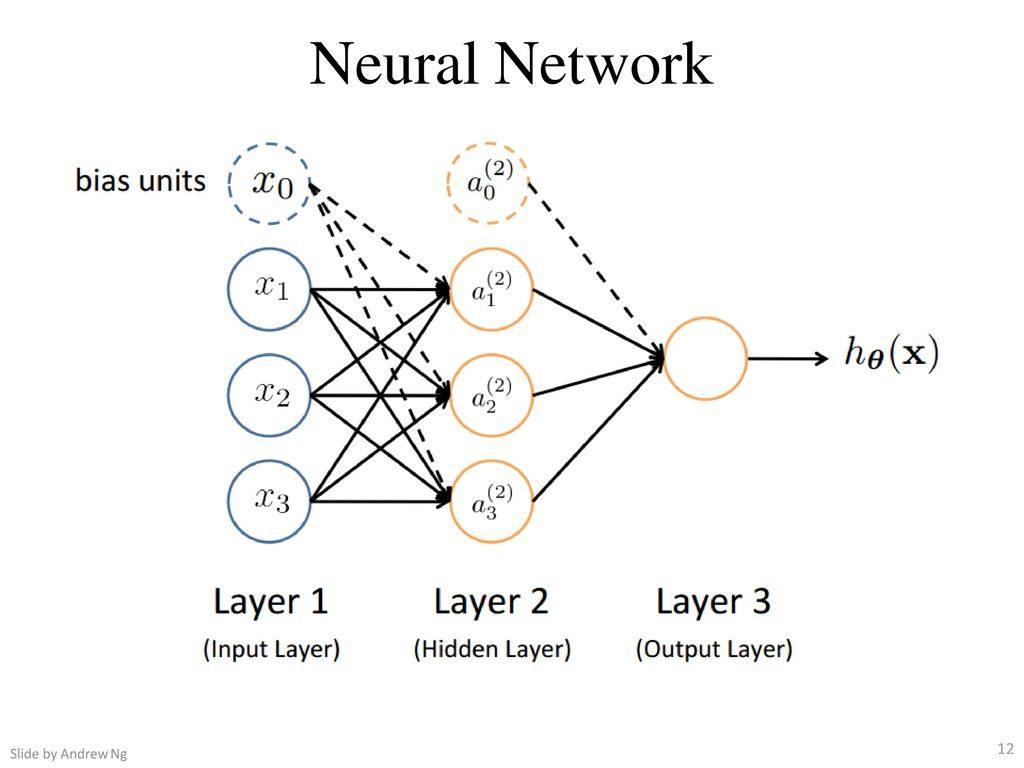
Figura 15: Representação de uma rede neural
Na Figura 15 podemos perceber que para gerar a saída (função hipótese) passamos por uma input layer e uma hidden layer. Com isso, podemos descrever uma equação para que possamos determinar o valor da saída partindo dos parâmetros acimas identificados.
\[ \large{} a _1 ^{(2)} = g( \Theta _{10} ^{(1)} x _0 + \Theta _{11} ^{(1)} x _1 + \Theta _{12} ^{(1)} x _2 + \Theta _{13} ^{(1)} x _3) \]
\[ \large{} a _2 ^{(2)} = g( \Theta _{20} ^{(1)} x _0 + \Theta _{21} ^{(1)} x _1 + \Theta _{22} ^{(1)} x _2 + \Theta _{23} ^{(1)} x _3) \]
\[ \large{} a _3 ^{(2)} = g( \Theta _{30} ^{(1)} x _0 + \Theta _{31} ^{(1)} x _1 + \Theta _{32} ^{(1)} x _2 + \Theta _{33} ^{(1)} x _3) \]
\[ \large{} h _{\Theta}(x) = a _1 ^{(3)} = g( \Theta _{10} ^{(2)} a _0 ^{(2)} + \Theta _{11} ^{(2)} a _1 ^{(2)} + \Theta _{12} ^{(2)} a _2 ^{(2)} + \Theta _{13} ^{(2)} a _3 ^{(2)}) \]
Percebe-se que a matriz \( \Theta \) é uma matriz de tamanho \( 3 \times 4 \) (3 = número de parâmetros na camada dois e 4 = número de parâmetros de entrada). Quando aplicamos a função sigmoide para cada uma das camadas, nós obtemos o nodo de ativação da próxima camada. Assim, a função hipótese é a função logística aplicada na soma dos valores dos nodos de ativação os quais são multiplicados pelo parâmetro da matriz \( \Theta ^{(2)} \) que contém os valores dos pesos da segunda camada de nodos.
Com isso, temos a seguinte definição:
Se uma rede neural tem \( s _j \) unidades na camada \( j \) e \( s _{j+1} \) unidades na camada \( j+1 \), então \( \Theta ^{(j)} \) terá dimensões \( s _{j+1} \times (s _j + 1) \).
Com as definições vistas acima, podemos introduzir uma implementação vetorizada das funções vistas. Para isso, iremos definir uma variável \( z _k ^{(j)} \) que engloba os parâmetros dentro da função \( g \). Assim, teríamos:
\[ \large{} a _1 ^{(2)} = g(z _1 ^{(2)}) \]
\[ \large{} a _2 ^{(2)} = g(z _2 ^{(2)}) \]
\[ \large{} a _3 ^{(2)} = g(z _3 ^{(2)}) \]
Em outras palavras, para a camada \( j=2 \), a função \( z \) seria:
\[ \large{} z _k ^{(2)} = \Theta _{k,0} ^{(1)} x _0 + \Theta _{k,1} ^{(1)} x _1 + \Theta _{k,2} ^{(1)} x _2 + \dots + \Theta _{k,n} ^{(1)} x _n \]
E a função vetorizada teria a forma:
\[ \large{} x = \begin{bmatrix} x _0 \\ x _2 \\ \dots \\ x _n \end{bmatrix} , z ^{(j)} = \begin{bmatrix} z _1 ^{(j)} \\ z _2 ^{(j)} \\ \dots \\ z _n ^{(j)} \end{bmatrix} \]
Com \( x = a ^{(1)} \) teremos:
\[ \large{} z ^{(j-1)} = \Theta ^{(j-1)} a ^{(j-1)} \]
Com essas manipulações temos que a função hipótese pode ser definida da seguinte forma:
\[ \large{} h _{\Theta}(x) = a ^{(j+1)} = g(z ^{(j+1)}) \]