Função Custo (Cost Function)

Nas seções anteriores, discutimos a implementação da função custo para a regressão linear. Entretanto, para a regressão logística, utilizaremos uma função hipótese voltada para os problemas de classificação. Na Figura 10 está representada a função logística que será utilizada para calcular a hipótese do problema. Essa função gera valores probabilísticos no intervalo \( [0,1] \) e, com isso, podemos calcular o valor da função custo de forma que possamos comparar a probabilidade da nossa hipótese ser igual a 1 com o resultado \( y \) esperado.

Para realizar essa comparação, devemos realizar algumas manipulações algébricas de forma que possamos definir uma função \( J(\theta) \) que calcule o custo. Abaixo, está descrita a intuição dessa manipulação.

\[ \large{} J(\theta) = \frac{1}{m} \sum _{i=1} ^m Cost(h _{\theta}(x ^{(i)}), y ^{(i)}) \]

\[ \large{} Cost(h _{\theta}(x ^{(i)}), y) = - \log (h _{\theta}(x)) \ se \ y=1 \]

\[ \large{} Cost(h _{\theta}(x ^{(i)}), y) = - \log (1 - h _{\theta}(x)) \ se \ y=0 \]

Dessa forma, podemos ter duas diferentes funções para a representação da função custo para a regressão logística. Como podemos ver na Figura 12 temos duas representações, para \( y=1 \) em azul e para \( y=0 \) em vermelho.

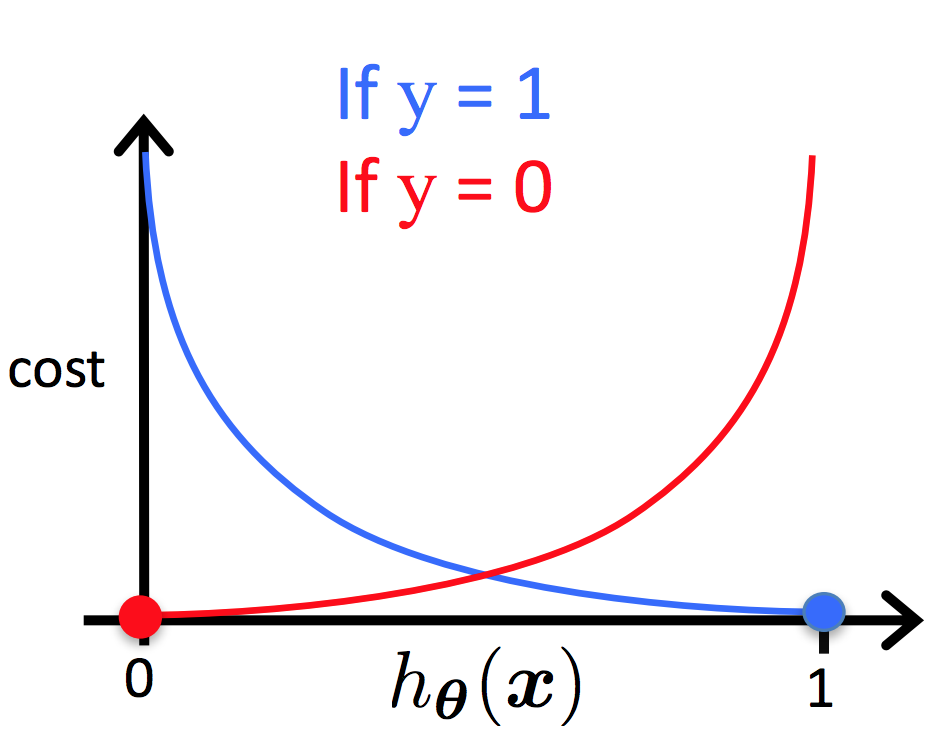
Figura 12: Representação da função custo da regressão logística

\[ \large{} Cost(h _{\theta}(x ^{(i)}), y) = 0 \ \ se \ \ h _{\theta}(x) = y \]

\[ \large{} Cost(h _{\theta}(x ^{(i)}),y) \rightarrow \infty \ \ se \ \ y=0 \ \ e \ \ h _{\theta}(x) \rightarrow 1 \]

\[ \large{} Cost(h _{\theta}(x ^{(i)}),y) \rightarrow \infty \ \ se \ \ y=1 \ \ e \ \ h _{\theta}(x) \rightarrow 0 \]

Podemos perceber que quando o valor da função custo é zero, então o valor da função hipótese é igual a \( y \). Além disso, quando a função custo tende ao infinito e o valor de \( y \) é igual a zero, o valor da função hipótese tende a um e se o valor de \( y \) é igual a um, a função hipótese tende a zero.

A fim de simplificar a função custo, podemos reescrevê-la da seguinte forma sem alterar o valor do resultado:

\[ \large{} Cost(h _{\theta}(x),y) = -y \cdot \log (h _{\theta}(x)) - (1-y) \cdot \log (1-h _{\theta}(x)) \]

Com isso, podemos generalizar a função custo de acordo com a expressão abaixo:

\[ \large{} J(\theta)=- \frac{1}{m} \sum _{i=1} ^m \Big[ y ^{(i)} \cdot \log (h _{\theta}(x ^{(i)})) + (1-y ^{(i)}) \cdot \log (1-h _{\theta}(x ^{(i)})) \Big] \]