Adam

Adaptative Moment Estimation (Adam) é outro método de otimização que computa taxas de aprendizado adaptativas para cada parâmetro, assim como AdaGrad e outros métodos de otimização.

Enquanto nos métodos que utilizam momentum, nós podemos pensar em uma bola descendo uma curva em direção ao ponto mínimo, Adam se comporta como se fosse uma bolsa pesada com atrito descendo essa superfície. Essa forma de minimização faz com que o erro de minimização seja o menor possível, ao mesmo tempo que o tempo de convergência seja pequeno.

Assim como os otimizadores que utilizam momentum, vistos nas seções anteriores, Adam utiliza uma média exponencial dos gradientes calculados anteriormente para definir a taxa de aprendizado. Com isso, a atualização dos parâmetros se dá de forma muito similar aos otimizadores que utilizam momentum.

A intuição da implementação do Adam é dividida em três etapas: momentum, correção de bias e AdaGrad.

Na primeira etapa - momentum - computamos as médias vetores momentum passados \( m _t \) e, na terceira etapa, os quadrados dos gradientes passados \( v _t \), respectivamente, como segue:

\[ \large{} m _t = \beta _1 m _{t-1} + (1 - \beta _1) \nabla _{\theta} J(\theta) \]

\[ \large{} v _t = \beta _2 v _{t-1} + (1 - \beta _2) \nabla _{\theta} J(\theta) ^2 \]

Onde \( m _t \) e \( v _t \) são, respectivamente, o momentum acumulado e o gradiente acumulado até um período \( t \).

Como, \( m _t \) e \( v _t \) são previamente, inicializados com 0's, foi observado que essas atualizações, principalmente nas etapas iniciais, tendem à zero e, especialmente quando a taxa de decaimento é baixa (ou seja, quando \( \beta _1 \) e \( \beta _2 \) estão próximos de 1).

Para isso, na segunda etapa neutralizamos essas tendências não previstas através de bias-correction. Para isso, calculamos o valor de \( m̂ _t \) para atualizar a direção de cada um dos parâmetros e, através dos valores dos gradientes de \( v̂ _t \), atualizamos efetivamente a otimização dos parâmetros. Assim, teremos:

\[ \large{} m̂ _t = \frac{m _t}{1 - \beta _1 ^t} \]

\[ \large{} v̂ _t = \frac{v _t}{1 - \beta _2 ^t} \]

Agora, só basta calcular as atualizações dos parâmetros \( \theta \) utilizando, por exemplo AdaGrad.

\[ \large{} \theta _{t+1} = \theta _t - \frac{\eta}{\sqrt{v̂ _t} + \epsilon} m̂ _t \]

Com isso, a otimização funcionaria corretamente com os parâmetros propostos para \( \beta _1 = 0.9 \) e \( \beta _2 = 0.999 \) e taxa de aprendizado \( \eta = 10 ^{-3} \) ou \( 5 \times 10 ^{-4} \)

Na figura abaixo, podemos perceber as diferenças entre os modelos de otimizações discutidos. Adam combina cada um dos modelos vistos anteriores a fim de otimizar a função custo.

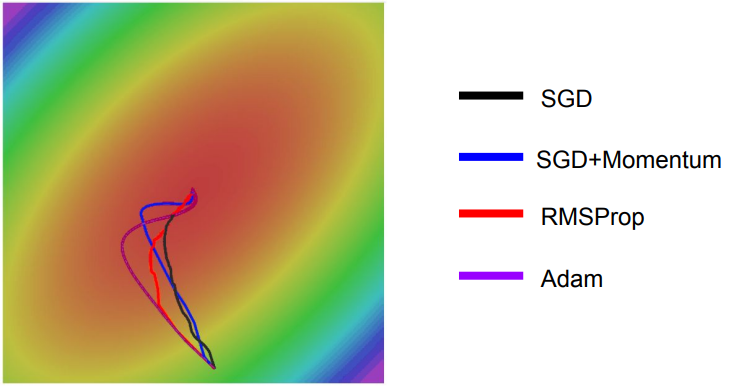
Figura 43: Comparação entre os modelos de otimização vistos. Percebe-se que Adam combinas os diferentes métodos.