Nesterov Accelerated Gradient (NAG)

O método NAG utiliza da mesma ideia vista na seção anterior, porém, como foi dito, desaceleramos a atualização dos parâmetros de forma a não ultrapassar de maneira muito significativa o valor de mínimo da função.

Na Figura 41, abaixo está representada a diferença no comportamento da atualização dos valores dos parâmetros.

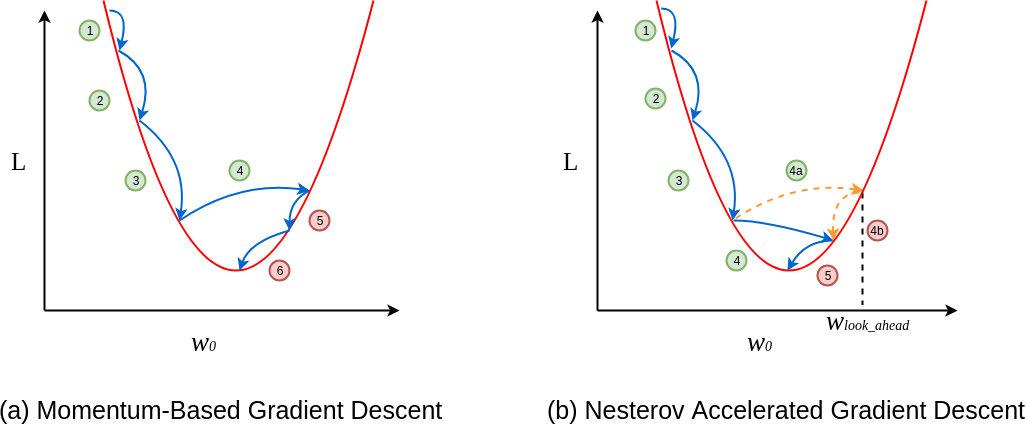
Figura 41: Exemplificação do método de Nesterov (à direita) para gradiente descendente utilizando momentum (à esquerda). Percebe-se que a cada passo, os valores da função custo diminuem tendendo ao mínimo. E quando esse valor se aproxima do mínimo, desacelera para facilitar a convergência.

Nesse método de otimização da função custo, primeiro olhamos para o onde o vetor atual momentum está apontando para, com ele, calcularmos o gradiente partindo desse ponto, como podemos verificar na Figura 42.

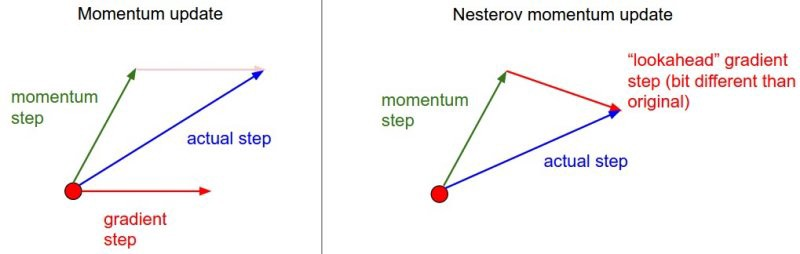
Figura 42: Representação da atualização dos vetores momentum utilizando o método de Nesterov. Na imagem à esquerda, verificamos a atualização do vetor momentum a partir de um determinado ponto. Na figura à direita verificamos a atualização do vetor momentum através do método de Nesterov, a partir do ponto onde o vetor está apontando.

O método de Nesterov utiliza o termo de momentum \( \rho v _{t-1} \) para atualizar os parâmetros \( \theta \). Assim, se computamos \( \theta - \rho v _{t-1} \) temos a aproximação da próxima posição dos parâmetros \( \theta \). Para calcularmos a atualização dos parâmetros, primeiro devemos definir a atualização de \( v _t \) utilizando o método de Nesterov, como descrito abaixo.

\[ \large{} v _{t} = \rho v _{t-1} + \alpha \nabla _{\theta} J(\theta - \rho v _{t-1}) \]

\[ \large{} \theta = \theta - v _t \]

onde, \( \rho \) é o termo definido como momentum (atrito, geralmente um valor em torno de 0.9), \( \alpha \) é a taxa de aprendizado e \( \nabla _{\theta} \) é o gradiente de \( J \) em relação aos parâmetros \( \theta \).

Assim, com a aplicação do método de Nesterov Momentum, o algoritmo de otimização da função converge muito mais rapidamente, evitando o problema de aproximação ruim da convergência no SGD.