Função Custo (Cost Function)

A função custo - também chamada de loss function - pode ser utilizada para medir a precisão da nossa função hipótese \( h:X \rightarrow Y \). A função custo utiliza da diferença média de todos os resultados da função hipótese com todos inputs de \( x \) e outputs de \( y \), como representado na Figura 5.

\[ \large{} J(\theta _0 , \theta _1) = \frac{1}{2m} \sum _{i=1} ^m (ŷ _i - y _i) ^2 = \frac{1}{2m} \sum _{i=1} ^m (h _{\theta}(x _i) - y _i) ^2 \]

Através dessa expressão podemos perceber que o objetivo principal da função custo é minimizar a diferença entre o resultado esperado a função hipótese e o valor de \( y \) através das entradas \( \theta _0 \) e \( \theta _1 \). Essa função também é conhecida como Squared error function ou Mean squared error.

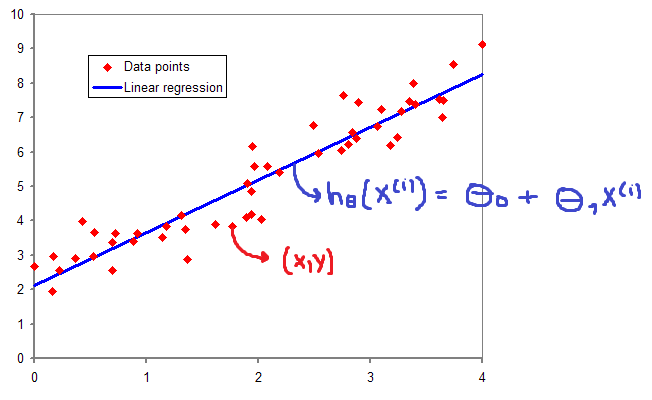
Figura 5: Representação da função custo

Dessa forma, temos quatro predefinições básicas:

• Hipótese: \( h _{\theta}(x) = \theta _0 + \theta _1 x \);

• Parâmetros: \( \theta _0 , \theta _1 \);

• Função Custo: \( J(\theta _0 , \theta _1) = \frac{1}{2m} \sum _{i=1} ^m (h _{\theta}(x _i) - y _i) ^2 \);

• Objetivo: \( \underset{\theta _0 , \theta _1} {min} \ J(\theta _0 , \theta _1) \)

Podemos utilizar linhas de contorno para representar a função de duas variáveis \( J(\theta _0 , \theta _1) \) em apenas duas dimensões como representado nas Figuras 6 e 7.

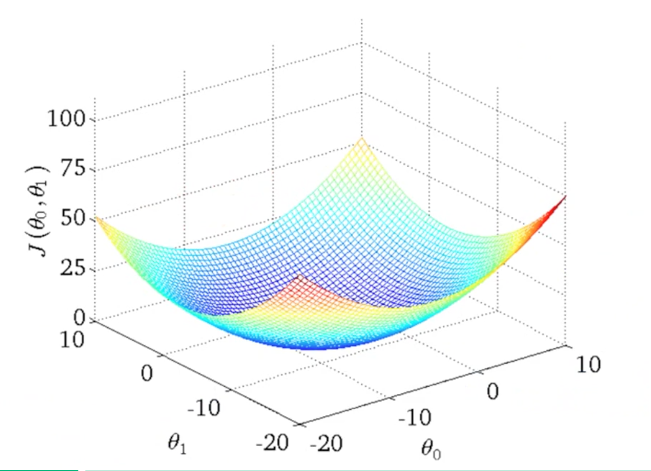
Figura 6: Representação da função custo através de visualização 3D

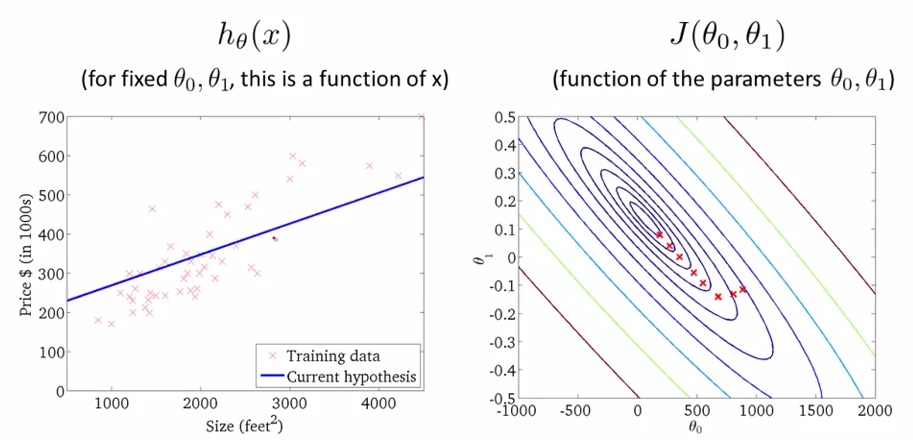
Figura 7: Representação da função custo através de linha de contorno

Os gráficos da Figura 7 minimizam a função custo ao máximo. O resultado de \( \theta _0 \) e \( \theta _1 \) tende a ficar em torno de 250 e 0.12, respectivamente. Em outras palavras, a melhor aproximação da função custo está mais no centro das linhas de contorno. Chamamos o método de minimização da função custo de método do gradiente descendente que será discutido na Seção Gradiente Descendente (Gradient Descent).