Curvas de aprendizado
Nesta seção iremos interpretar gráficos que representam curvas de aprendizado analisando os valores de \( J _{train}(\theta), J _{cv}(\theta) \) e \( J _{test}(\theta) \) para concluir se o treino está bem ajustado, com overfitting ou underfitting.
Em primeira análise, sabemos que para uma quantidade pequena de dados de entrada o valor do erro esperado é próximo de zero, pois o modelo aprende cerca de 100% do conjunto de treino. Porém, quando aumentamos o tamanho do conjunto de treino este erro tende a aumentar, muitas vezes, tanto para o conjunto de treino, quanto para o conjunto de teste. Para isso, podemos analisar dois tipos de situações esperadas: high bias e high variance.
Na representação a seguir que representa o erro da função \( J \) para casos de treino e teste de acordo com o grau do polinômio \( d \). Percebe-se que quanto maior o grau do polinômio, menor é a taxa de erro no conjunto de treino e maior é a taxa de erro no conjunto de teste, e quanto menor o grau do polinômio maior é a taxa de erro do conjunto de treino e maior é a taxa de erro do conjunto de teste. Assim, devemos ajustar o grau do polinômio de forma que ele seja grande suficiente para evitar os casos de underfitting e overfitting.
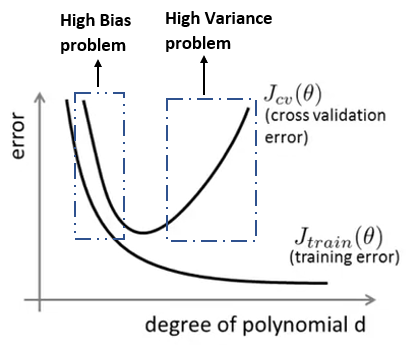
Figura 25: Representação das curvas \( J _{cv}(\theta) \) e \( J _{train}(\theta) \) relacionando o grau do polinômio \( d \) com a taxa de erro de cada uma dessas funções.