Gradiente Descendente (Gradient Descent)

O método do gradiente descendente pode ser utilizado para minimizar o valor de uma função. Utilizaremos esse método a fim de minimizar a função \( J(\theta _0 , \theta _1) \).

Podemos representar esse método a partir de um gráfico em três dimensões, onde \( \theta _0 \) está no eixo \( x, \theta _1 \) está no eixo \( y \) e o valor da função \( J(\theta _0 , \theta _1) \) está no eixo \( z \), conforme está representado na Figura 8. Os pontos no gráfico são os resultados da função custo utilizando a função hipótese \( h(x) \) com as entradas \( \theta _0 \) e \( \theta _1 \).

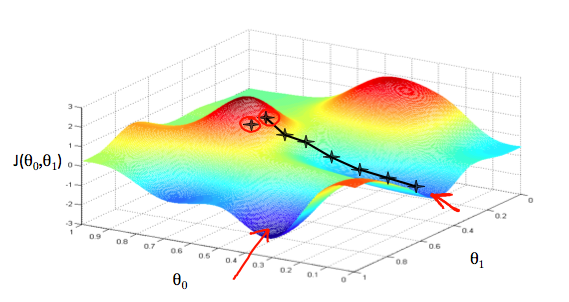
Figura 8: Representação da função gradiente descendente

O método de minimização utilizando a função gradiente descendente pode ser pensado como um algoritmo, que para cada ponto, a partir do inicial, dado como entrada, escolhe a descida mais íngreme do valor de \( J(\theta _0 , \theta _1) \) na função através de derivadas parciais e um valor \( \alpha \) (learning rate) que determinará a distância entre cada descida. Obtemos sucesso, quando a função custo estiver em um dos mínimos do gráfico, como representado pelas setas vermelhas na Figura 8.