Camadas de uma ConvNet
Como foi descrito acima, uma ConvNet é uma sequência de camadas que transforma um volume de ativações em outro através de uma função de diferenciação. Para isso, utilizamos camadas específicas para realizar o treinamento de uma ConvNet, dentre elas: Convolutional layer, Pooling layer e Fully-connected layer. Esta última, exatamente como uma rede neural regular.
A principal diferença entre uma dense layer e uma convolutional layer é que as camadas densas detectam padrões globais, enquanto camadas convolucionais detectam padrões locais.
Para a melhor compreensão será utilizado um exemplo CIFAR-10 [1] o qual consiste em uma base de dados com 60 mil imagens de tamanho 32x32 separadas em 10 classes. O conjunto de dados é separado em 50 mil para usado para treino e 10 mil para teste.
Uma ConvNet para classificar as imagens de CIFAR-10 tem a seguinte estrutura, detalhada abaixo:
- Input [32x32x3]: recebe um vetor dos valores dos pixels da imagem. Neste caso a imagem tem largura 32, altura 32 com três canais de cores (RGB);
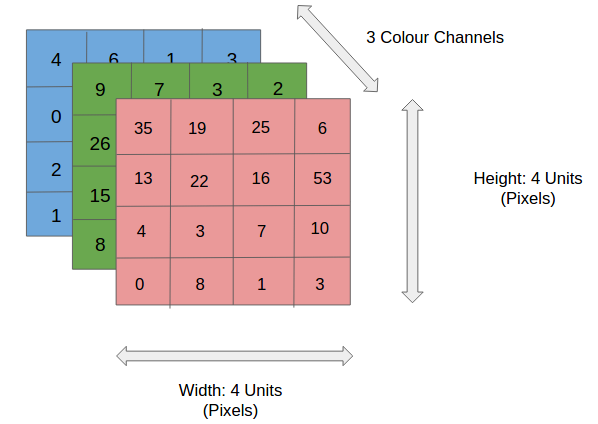
Figura 44: Representação de uma camada de input de uma rede neural convolucional. Podemos perceber, que na imagem representada temos uma imagem de tamanho 4x4 com três canais de cores RGB e cada valor de cada pixel corresponde a um valor em cada uma dessas escalas de cores.
- Conv Layer: computa a saída dos neurônios que estão conectados a regiões de entrada. Cada um computa um produto escalar entre os pesos e a uma região as quais eles estão conectados no volume de entrada. Isso pode resultar em um volume como [32x32x12] se desejarmos utilizar 12 filtros kernel. Este filtro possui um tamanho que varre a imagem através de strides - distância entre duas varreduras do filtro - gerando uma nova imagem de mesmo tamanho, porém com esse filtro aplicado;
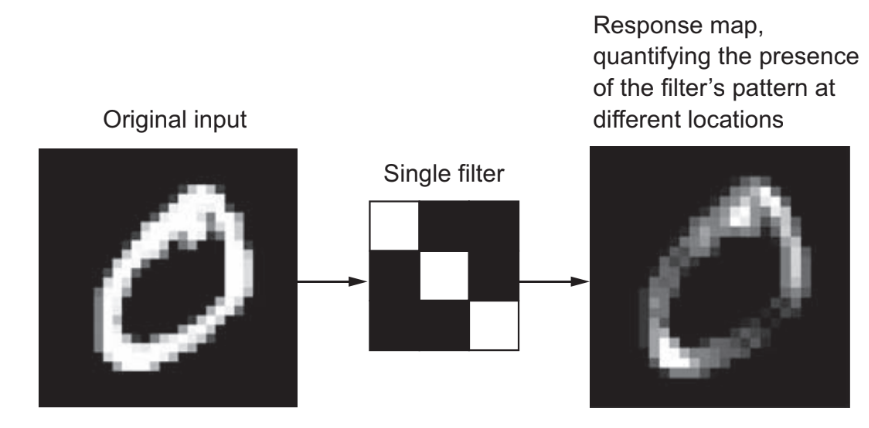
Figura 45: Representação da utilização de um filtro (kernel) para mapear os valores da imagem dada como entrada. Percebe-se que o filtro utilizado mantém as bordas da imagem de entrada.
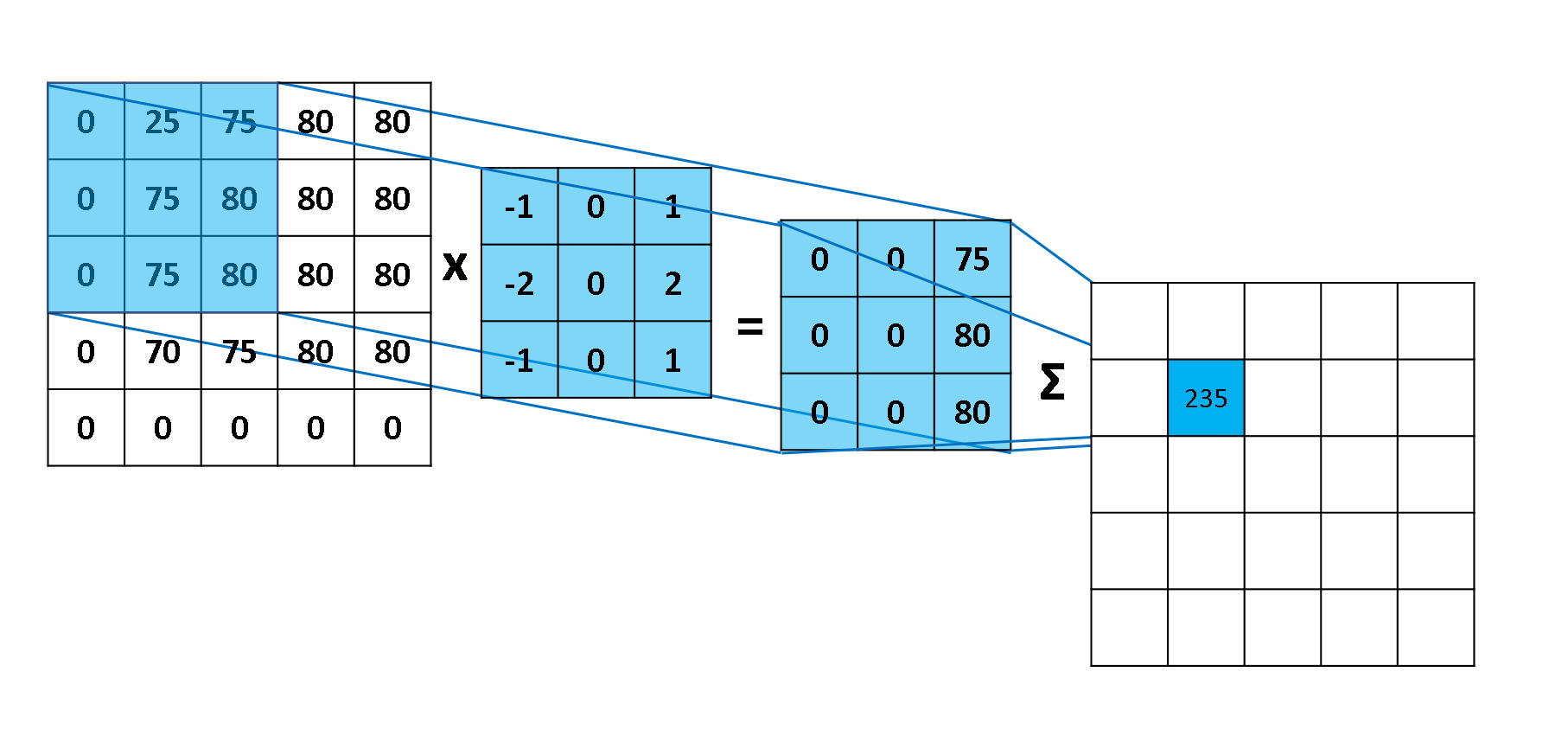
Figura 46: Representação das operações realizadas por um filtro a partir de uma imagem. O filtro (3x3) multiplica os valores da imagem (5x5) pelos seus respectivos valores até gerar uma saída correspondente de tamanho 3x3. Esses valores retornados são somados e adicionados ao respectivo pixel da imagem (5x5) camada seguinte com o filtro aplicado.
-
ReLU Layer: computa a função de ativação;
-
Pool Layer: computa uma operação de redução da resolução ao longo das dimensões, resultando em um volume como [16x16x12];
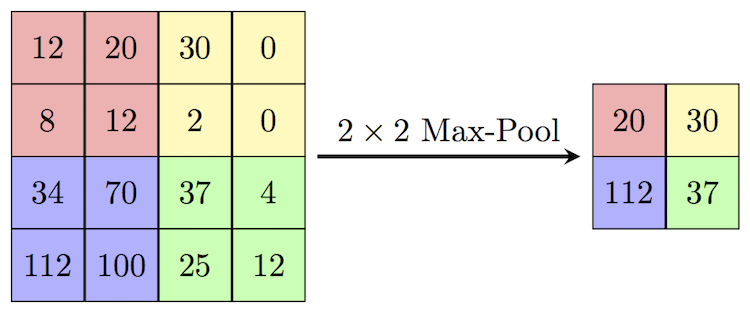
Figura 47: Representação de uma operação de pooling. Na figura, utiliza-se o método de max-pooling com um filtro de tamanho 2x2 o qual escolhe o maior valor do pixel que se encontra dentro do filtro.
- FC Layer: computa as pontuações das classes, resultando em um volume de tamanho [1x1x10], onde cada um dos 10 números representa uma categoria da base de dados CIFAR-10
Abaixo, na Figura 48 está representado, esquematicamente uma ConvNet voltada para a base de dados CIFAR-10. Nela, percebemos as operações que foram realizar ao longo do processamento de convolução e de aprendizado da classificação.
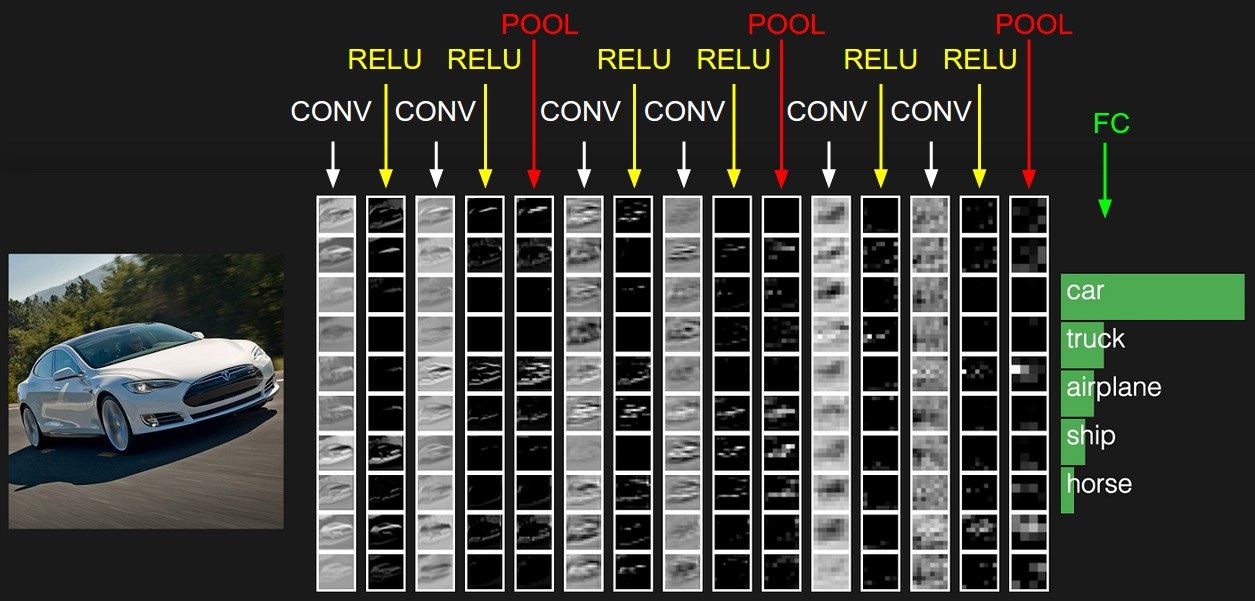
Figura 48: Representação de uma ConvNet para a base de dados CIFAR-10
Além disso, uma camada de convolução de uma ConvNet recebe alguns outros parâmetros que serão descritos a seguir:
-
Aceita um volume de tamanho: \( W _1 \times H _1 \times D _1 \);
-
Requer quatro hiperparâmetros:
-
Número de filtros (kernels): \( K \)
-
Tamanho do filtro: \( F \)
-
Stride (distância entre duas posições consecutivas do filtro): \( S \)
-
Tamanho da borda (zero-padding): \( P \)
-
-
Produz um volume de: \( W _2 \times H _2 \times D _2 \) onde:
-
\( W _2 = \frac{(W _1 - F + 2P)}{S + 1} \)
-
\( H _2 = \frac{(H _1 - F + 2P)}{S + 1} \)
-
\( D _2 = K \)
-
Geralmente, uma inicialização comum para esses parâmetros é \( F=3 , \ S=1 \) e \( P=1 \), porém esses parâmetros podem ser modificados de acordo com a intenção de treino da ConvNet.
Da mesma forma, uma camada de pooling de uma ConvNet recebe alguns parâmetros a seguir descritos:
-
Aceita um volume de tamanho: \( W _1 \times H _1 \times D _1 \);
-
Requer dois hiperparâmetros:
-
Tamanho do filtro: \( F \)
-
Stride: \( S \)
-
-
Produz um volume de: \( W _2 \times H _2 \times D _2 \) onde:
-
\( W _2 = \frac{(W _1 - F)}{S + 1} \)
-
\( H _2 = \frac{(H _1 - F)}{S + 1} \)
-
\( D _2 = D _1 \)
-
Assim, percebemos que uma ConvNet é simplesmente uma lista de camadas que transformam um volume de entrada (neste caso uma imagem) e um outro volume de saída (neste caso os valores das classes).