Long Short-Term Memory (LSTM)
As arquiteturas de LSTMs são utilizadas para resolver os problemas de dificuldade de memorização de longas sequências causadas pelo desaparecimento do gradiente.
A LSTM é uma RNN que memoriza os valores em intervalos arbitrários, sendo, assim, muito adequada para processar e prever séries de valores temporais com intervalos de tempo de duração desconhecida. Como pode-se verificar na Figura 72, a LSTM possui uma estrutura de cadeia que contém quatro redes neurais e diferentes blocos de memória chamados ”células”.
Para cada período de tempo, a LSTM retorna dois valores: \( h _t \) e \( c _t \) que são, respectivamente, os valores da hipótese de cada período e os valores da célula de cada período. Ambos valores possuem o mesmo tamanho \( n \). A célula guarda as informações de longo prazo da rede neural, enquanto a hipótese é o valor gerado de determinado período de tempo.
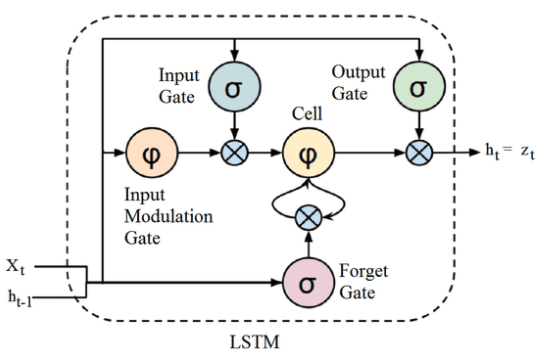
Figura 72: Representação de uma arquitetura LSTM. Percebe-se que existem três gates (input, forget e output) e uma célula, onde são realizadas as operações de memorização.
Com isso, uma LSTM consegue ler, apagar e escrever informações da célula. Essas informações são controladas através dos portões (gates) que, para cada período de tempo, eles podem estar fechados (0) ou abertos (1). Esses portões são dinâmicos, ou seja, os seus valores são computados de acordo com o contexto da sequência passada como entrada. A seguir, estão listados e definidos cada um dos gates representados na Figura 72 acima.
- Forget Gate: as informações que não são mais úteis no estado da célula são removidas através do forget gate. Os valores de \( x ^{< t >} \) e \( a ^{< t-1 >} \) são alimentadas no gate e multiplicadas pelas matrizes \( W \) , resultando em um valor binário após a passagem pela função de ativação. Caso a saída seja 0, o valor é esquecido e caso seja 1 o valor é mantido para uso futuro.
\[ \large{} f _t ^1 = \sigma (W _{f ^1} \cdot [a ^{< t-1 >} x ^{< t >}] + b _{f ^1}) \]
- Input Gate: as informações úteis para o estado da célula é feita pelo input gate. Primeiro, a informação é regulada através da função sigmoide, filtrando os valores, e, depois um vetor de valores criados usando a função \( tanh \) retorna valores entre -1 a 1, que contém todos os valores possíveis para \( x ^{< t >} \) e \( a ^{< t-1 >} \). Em seguida, os valores do vetor e os valores regulados são multiplicados para obter as informações úteis.
\[ \large{} f _t ^1 = \sigma (W _{f ^2} \cdot [a ^{< t-1 >} x ^{< t >}] + b _{f ^1}) \odot tanh (W _{f ^2} \cdot [a ^{< t-1 >} x ^{< t >}] + b _{f ^2}) \]
- Output Gate: as informações úteis da célula atual que podem ser usadas nos estados seguintes são extraídas através do output gate. Um vetor é, primeiramente, gerado aplicando a função \( tanh \) na célula e, depois, essa informação é regulada através da função sigmoide filtrando os valores a serem lembrados. Os valores do vetor e dos valores regulados são multiplicados e são enviados como saída para a célula seguinte.
\[ \large{} h' _t = \sigma (W _{h' _t} \cdot [a ^{< t-1 >} x ^{< t >}] + b _{h' _t}) \odot tanh (c _t) \]
No entanto, LSTMs possuem um problema similar aos modelos de RNNs. Quando as sentenças são muito grandes, LSTMs não funcionam muito bem. Isso acontece porque o valor de uma célula muito anterior à célula atual decresce exponencialmente e isso potencializa a perda de informação e a falta de controle do processo. Em geral, RNNs e LSTMs possuem três problemas:
-
A computação sequencial inibe a paralelização. Em outras palavras não podemos paralelizar tarefas em uma RNN ou em uma LSTM devido ao fato de que seu processamento é sequencial;
-
Sem modelagem explícita de dependências de longo e curto alcance;
-
A distância entre as posições é linear.
Contudo, mesmo com a memorização mais eficiente, LSTMs não resolvem efetivamente o problema do desaparecimento do gradiente, justamente por, ainda assim, se tratar de uma sequência. Atualmente, esse problema pode ser resolvido através da utilização de arquiteturas de redes neurais residuais, ou ResNets [8].