Forward pass
O principal objetivo dessa fase é calcular os valores de cada neurônio da nossa rede neural aplicando uma série de dot products (multiplicações entre vetores) e funções de ativação a fim de atingirmos a camada final da rede.
Por exemplo, se temos os seguintes valores de entrada \( x _i \) e a saída esperada \( y \), de acordo com a tabela a seguir:
Tabela 3: Valores hipotéticos de entrada para a rede neural seguindo uma tupla do tipo \( (x, y) \)
| \( x _0 \) | \( x _1 \) | \( x _2 \) (bias) | \( y \) |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
Cada um desses valores de \( x _i \) estarão presentes na input layer da rede neural. E para cada um desses valores, serão realizados dot products entre as entradas de cada camada seguido pelo cálculo da função de ativação. Esta ideia está exemplificada na Figura 22 a seguir.
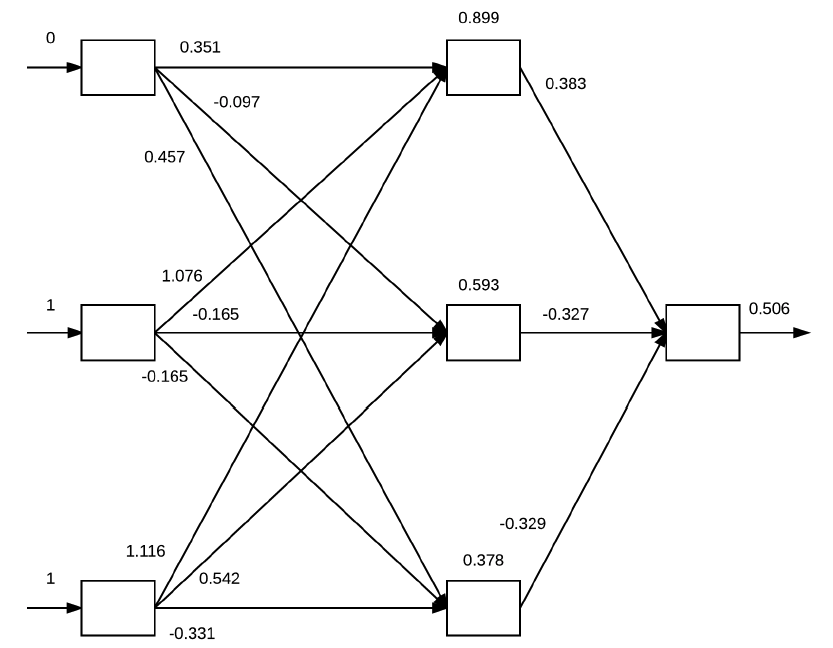
Figura 22: Exemplificação do algoritmo backpropagation a partir dos inputs definidos na Tabela 3. Na input layer estão os valores de \( x \) definidos. Os valores das arestas são inicializados aleatoriamente e representam os pesos. Na hidden layer estão os valores calculados a partir dos dot products e das aplicações das funções de ativação (neste caso, sigmoide) e na output layer o valor calculado pela função custo.
A partir dos valores de entrada baseados na Tabela 3 e os pesos que foram inicializados aleatoriamente, para cada um desses valores executamos as seguintes operações de dot products e ativações utilizando a função \( g(z) \) sigmoide:
-
\( g((0 \times 0.351) + (1 \times 1.076) + (1 \times 1.116)) = 0.899 \)
-
\( g((0 \times 0.097) + (1 \times 0.165) + (1 \times 0.542)) = 0.593 \)
-
\( g((0 \times 0.457) + (1 \times 0.165) + (1 \times 0.331)) = 0.378 \)
Os valores dos neurônios das hidden layers são atualizados de acordo com essas operações e, com eles podemos aplicar mais uma vez as mesmas operações para cada um dos valores atualizados para gerarmos o valor da output layer.
\[ \large{} g((0.899 \times 0.383) + (0.593 \times -0.327) + (0.378 \times -0.329)) = 0.506 \]
A saída é, portanto, \( 0.506 \), o que representa um valor de probabilidade de 50,6%. Contudo, percebe-se que a rede neural não tem muita confiança a respeito do valor gerado, então, para que a rede neural realmente aprenda precisamos realizar a minimização da função custo através da etapa de Backward pass.