PixelRNN

Através da utilização de modelos probabilísticos de densidade, como por exemplo Distribuição Normal, consegue gerar imagens começando através de um canto e calculando qual é o valor do próximo pixel que mais faz sentido de acordo com os pixels previamente gerados e com um valor de probabilidade.

Para processar a relação entre geração do pixel e valor de probabilidade, utilizamos de modelos que funcionam bem com sequências, como por exemplo, Redes Neurais recorrentes (RNNs).

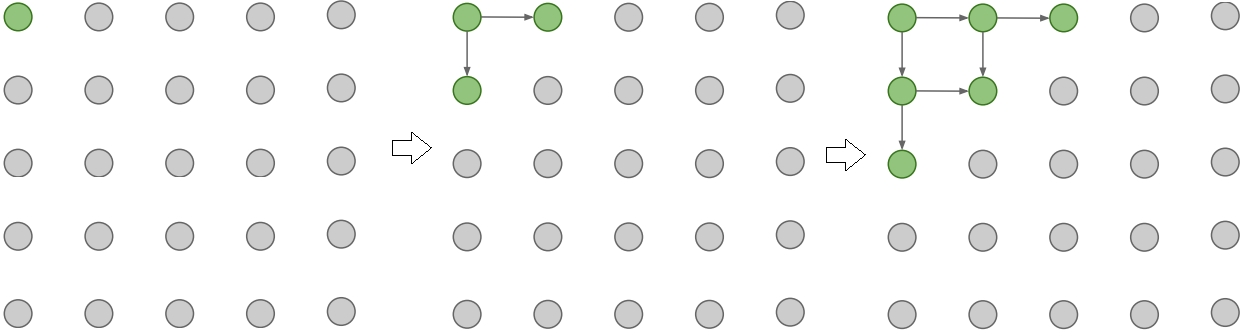
Figura 89: Geração de pixels utilizando PixelRNN. A partir de um pixel do canto da imagem, o modelo começa a gerar, sequencialmente outros pixels baseados nos valores de probabilidade e nos valores dos pixels previamente gerados.

A rede neural "varre" a imagem gerando, linha a linha e pixel a pixel a cada período de tempo, o que pode ser, muitas vezes, muito demorado. Os valores dos pixels são gerados baseando-se nos valores de probabilidade gerados através de uma distribuição que é escrita a partir do produto condicional das distribuições e os valores gerados são compartilhados através da imagem.

O objetivo, então é calcular a probabilidade \( p(x) \) para cada pixel da imagem de tamanho \( nxn \). Assim, a probabilidade pode ser escrita da seguinte forma:

\[ \large{} p(x) = \prod _{i=1} ^{n ^2} p(x _i|x _1, \dots , x _{i-1}) \]

A equação acima é a probabilidade do \( i \)-ésimo pixel dada a probabilidade de todos os pixels pre- viamente gerados. Essa geração se dá linha a linha e pixel por pixel. Além disso, cada pixel \( x _i \) é juntamente determinado por todos os três canais de cores RGB. Assim, a probabilidade condicional do \( i \)-ésimo pixel se torna:

\[ \large{} p(x _{i,R}|X _{<i}) p (x _{i,G}|X _{<i}, x _{i,R}) p (x _{i,B}|X _{<i}, x _{i,R}, x _{i,G}) \]

Portanto, cada cor é condicionada sobre as outras cores e os pixels previamente gerados.

Contudo, um dos principais problemas desse tipo de implementação é a velocidade. Como geramos cada pixel sequencialmente, isso pode ser extremamente lento de acordo com a complexidade da saída. Para resolver esse problema de otimização, podemos utilizar um método similar e paralelizável utilizando ConvNets, chamado PixelCNN.