Mini-batch Gradient Descent

Mini-batch Gradient Descent muitas vezes, pode ser mais eficiente que o SGD. Ao invés de usarmos todos os \( m \) exemplos de treino, como no método clássico, ou apenas um exemplo no SGD, usaremos algo entre essas duas opções. Selecionaremos \( b \) exemplos de treino. O valor de \( b \), geralmente está entre 2-100.

Na figura a seguir, podemos verificar as diferenças entre o SGD e o Mini-batch Gradient Descent. Na imagem, percebe-se que o método Mini-batch converge mais rapidamente, principalmente devido ao fato de processar os dados em batches de forma vetorizada.

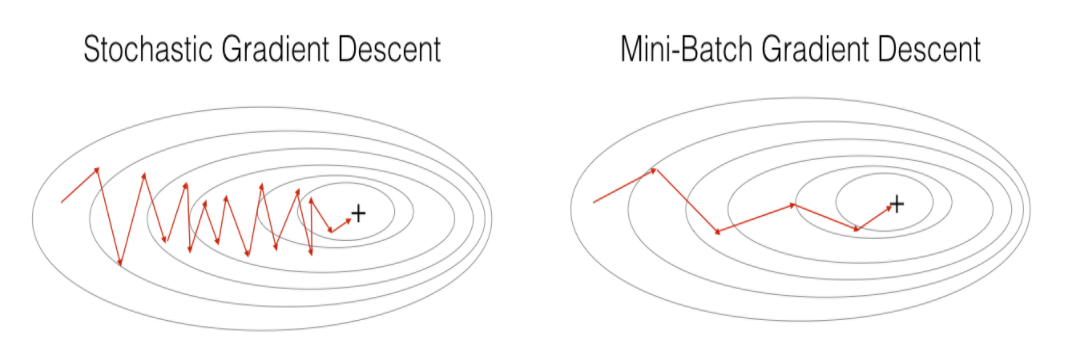
Figura 39

Por exemplo, se \( b = 10 \) e \( m = 1000 \), teremos o seguinte algoritmo:

Algorithm 11 Algoritmo Mini-batch Gradient Descent

1: procedure

2:   Aleatoriamente,"misturar" o conjunto de dados

3:   for \( i = 1,11,21,31, \dots , 991 \) do

4:    \( \theta _j := \theta _j - \alpha \frac{1}{10} \sum _{k=i} ^{i+9} (h _{\theta}(x ^{(k)}) - y ^{(k)}) \cdot x _j ^{(k)} \)

5:   end for

6: end procedure

Nesse algoritmo, estamos simplesmente somando dez exemplos por vez. A principal vantagem em computar mais de um exemplo por vez (em batches) é que podemos usar implementações vetorizadas sobre os exemplos em \( b \).