Classificação Multiclasse
Em problemas que são utilizados redes neurais, comumente são utilizados métodos de resolução desses problemas de forma multiclasse. Em outras palavras, a rede neural não terá apenas uma função hipótese como saída, \( h _{\Theta}(x) \) nesses casos será um vetor que pertence a \( \mathbb{R} ^n \).
Na Figura 18 abaixo podemos perceber que a rede neural foi construída com o objetivo de resolver um problema de classificação multiclasse, pois percebemos que a camada verde, abaixo ("layer 4"), que representa a função hipótese, é um vetor que pertence a \( \mathbb{R} ^4 \)
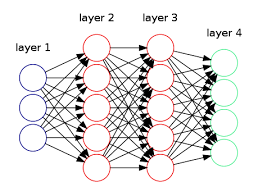
Figura 18: Representação de uma rede neural com classificação multiclasse
É possível escrever um programa de visão computacional para que possamos diferenciar pedestres, carros, motos e caminhões. Assim, teremos quatro nodos na output layer que representam cada um dos tipos de automóveis descritos.
\[ \large{} h _{\Theta}(x) ^1 \approx \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} , \ h _{\Theta}(x) ^2 \approx \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} , \ h _{\Theta}(x) ^3 \approx \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} , \ h _{\Theta}(x) ^4 \approx \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \]
Onde \( h _{\Theta}(x) ^1 \) representa um pedestre, \( h _{\Theta}(x) ^2 \) representa um carro, \( h _{\Theta}(x) ^3 \) representa uma moto e \( h _{\Theta}(x) ^4 \) representa um caminhão. Dessa forma, a rede neural poderia ser modelada, em forma vetorial, da seguinte forma:
\[ \large{} \begin{bmatrix} x _0 \\ x _1 \\ x _2 \\ \dots \\ x _n \end{bmatrix} \rightarrow \begin{bmatrix} a _0 ^{(2)} \\ a _1 ^{(2)} \\ a _2 ^{(2)} \\ a _3 ^{(2)} \\ \dots \end{bmatrix} \rightarrow \begin{bmatrix} a _0 ^{(3)} \\ a _1 ^{(3)} \\ a _2 ^{(3)} \\ a _3 ^{(3)} \\ \dots \end{bmatrix} \rightarrow \dots \rightarrow \begin{bmatrix} h _{\Theta}(x) _1 \\ h _{\Theta}(x) _2 \\ h _{\Theta}(x) _3 \\ h _{\Theta}(x) _4 \end{bmatrix} \]